预备知识#

量子场论简介#

量子场论是迄今为止描述基本粒子，如电子，光子，夸克，黑格斯玻色子等的相互作用规律的最成功无理论。不仅如此，量子场论的方法和概念也在如经典和量子引力，凝聚态物理，原子分子物理，宇宙学等物理学的各个分支中获得广泛而重要的应用。从某种意义上说，量子场论是整个现代物理学的理论框架，其重要性不亚于微积分之于经典物理学。这样一个如此成功的理论是从何而来的？发展它的原初动机是什么？它有哪些成功的应用和局限？量子场论作为描述自然界迄今为止最为复杂的理论框架，我们不太可能在一个学期内彻底掌握它，但至少希望经过这一门课的学习，能为同学们打开一扇窗户，也为将来更深入地掌握量子场论的概念和方法，乃至做出有意义的工作奠定基础。

什么是量子场论？#

  • 经典场的量子化

    • 正则量子化

    • 路径积分量子化

    • 形变量子化、几何量子化、…

  • {算符,关联函数}

    • 构造性量子场论

    • 代数量子场论

  • 。。。

物理学分支

微观机制

场论描述

场激发

粒子物理

规范对称性

相对论性场论

基本粒子

凝聚态物理

多体量子力学，例：晶格振动，自旋波

非相对论场论

声子，磁振子

临界现象与相变

统计场论

引力波

广义相对论

微扰引力场

引力子

量子引力

弦论？？？

世界面场论

冷原子物理

核力

非相对论性场论

核物理

核力

核有效场论

通过这门课程的学习你将会了解到：

  • 场的量子化和粒子激发

  • 量子力学和相对论要求反粒子的存在

  • 自旋-统计定理

  • 对称性和守恒律

  • 规范对称性的起源

  • 自旋的起源

  • 辐射修正和无穷大

  • 从量子场论到经典势

  • 量子场的真空能

  • 跑动耦合常数和重整化群流

  • 外尔，狄拉克和马约拉纳旋量

此讲义漏洞甚多，欢迎同学们指出！

预备知识（持续更新中）#

基本常数#

在《物理学的魅力》一书中，诺贝尔奖得主格拉肖用如下一幅图展示了我们宇宙的浩瀚结构和神秘的统一性：

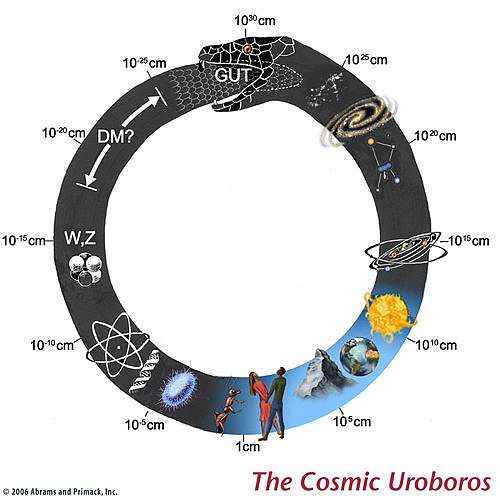
_images/glashaw.jpg

Fig. 1 格拉肖之蛇#

自然宇宙结构的绝大部分特征都可以用一些基本常数来描述。三个最基本常数是(在自然单位制下)：

  • 光速\(c = 3 \times 10^8 \text{m/s}\)

  • 普朗克常数\(\hbar = 1.05 \times 10^{-34} \text{J s}\)

  • 牛顿引力常数\(G = 6.67 \times 10^{-11} \text{m}^3 \text{kg}^{-1} \text{s}^{-2}\)

这三个常数的基本地位体现在无法通过他们的组合构造无量纲常数。从他们出发可以得到长度，时间，质量三个基本量纲：

  • 普朗克长度：\(l_p = \sqrt{\frac{\hbar G}{c^3}} = 1.6 \times 10^{-35} \text{m}\)

  • 普朗克时间：\(t_p = \sqrt{\frac{\hbar G}{c^5}} = 5.4 \times 10^{-44} \text{s}\)

  • 普朗克质量：\(m_p = \sqrt{\frac{\hbar c}{G}} = 2.2 \times 10^{-8} \text{kg}\)

从他们出发，可以得到任何带量纲物理量。

自然法则的一个奇妙之处在于这三个基本常数取值的偶然性以光速为例，我们看看他的改变对自然界会发生何种影响。光与电磁波属于同一类现象，因此我们的问题是光速的改变会如何影响光与物质相互作用，物质的稳定性，和能量的转化问题。

让我们想象光速比现有值大十个数量级，\(c = 3 \times 10^{18} \text{m/s}\)，但其他的基本常数保持不变。换句话说，我们看的是一个极端非相对论或者说伽利略宇宙。这时世界会变成什么样子？首先能知道的是化学现象将不会有太大改变，这是因为化学性质主要由原子壳层电子的性质所决定。因此我们需要从原子物理层面去寻找改变。

  • 物质的结构

原子的稳定结构源自电子和原子核的吸引库伦势。表面上看，库伦势由光子传递，因此光速的改变会影响库伦势的传递速度。但实际上，在量子电动力学中，电磁场和物质相互作用可以通过拉氏量中如下一项描述：

(1)#\[\begin{equation} \mathcal{L}_{\text{int}} \propto A_\mu j^\mu \end{equation}\]

其中\(A^\mu = (\phi/c, \boldsymbol{A})\)是四维矢势，\(j^\mu = (\rho c, \boldsymbol{j})\)是四维电流。可以看见，对非相对论项，也就是势的零分量，光速因子刚好抵消了。因此库伦势将不受光速改变的影响。这也可以从氢原子的玻尔半径公式中看出来：

(2)#\[\begin{equation} r_B = \frac{4 \pi \varepsilon_0 \hbar^2}{e^2 m_e} \end{equation}\]

因此在伽利略极限下我们的原子结构没发生大的改变。

  • 光与物质相互作用

对于一个具有确定能量\(E\)的光量子，其动量为\(p = E/c\)，波长\(\lambda = h/p = h c/E\)。因此光速增加会导致动量减小，波长增加，但频率\(\omega = E/\hbar\)不变。

首先我们来看物质如何发光。 自然界中发光的一个重要机制是激发态原子跃迁掉回更低能态。自发辐射概率正比于光子的相空间：

(3)#\[\begin{equation} d^3 k \to \frac{1}{c^3} d^3 k \end{equation}\]

偶极近似下的自发辐射率公式为 \(\Gamma_{\rm rad} (\omega) = \frac{\omega^3 n |\mu_{12}|^2 }{3 \pi \varepsilon_0 \hbar c^3}\)

因此如果光速增加10个数量级，自发辐射率将降低30个数量级！原子的光学辐射时间将达到宇宙年龄量级！

我们再来看这时光会如何被物质散射。光与自由电子的散射截面有汤姆生截面公式描述：

(4)#\[\begin{equation} \sigma_{\rm tot} = \frac{8 \pi}{3} \left( \frac{e^2}{4 \pi \varepsilon_0 m_e c^2}\right)^2 \end{equation}\]

随着光速增加10个数量级，散射截面将减小40个数量级！这意味着光与物质几近退耦！

  • 能量转化

一个重要的能量转换形式是机械能到电能的转换。在电动力学中，这依赖于如下麦克斯韦方程：

(5)#\[\begin{equation} \nabla \times \boldsymbol{B} = \mu_0 \boldsymbol{j} + \cdots \end{equation}\]

当\(c \to \infty\)时，\(\mu_0 \to 0\)，因此磁场和电流也退耦，通常意义上的发动机将不存在。

\(c\to \infty\)对应于伽利略极限，大家看到，尽管光速似乎对人们日常生活意义不大，但真的让其趋于无穷时，整个世界发生了巨大的改变。

如果光速不是增加而是减少又会怎样？伽莫夫的科普作品《物理世界奇遇记》描述了这样一个假想世界，其中的光速是如此之低，以至于骑着自行车就能观测到相对论尺缩效应。

_images/tompkins.jpg

Fig. 2 《物理世界奇遇记》插图#

当然，如果仔细想一想的话如此低的光速世界早就发生了巨变了。这次我们考虑一个与动力学相关的量，精细结构常数：

(6)#\[\begin{equation} \alpha = \frac{e^2}{4 \pi \varepsilon_0 \hbar c} \end{equation}\]

在粒子物理标准模型中，\(\alpha \sim 1/137\)。光速只需要降低100倍，\(\alpha\)就几乎接近一。氢原子的结合能是

(7)#\[\begin{equation} E_B = \frac{m e^4}{ 32 \pi^2 \varepsilon_0^2 \hbar^2} = \frac{1}{2} m c^2 \alpha^2 \end{equation}\]

对于充分大的\(\alpha\)，氢原子的结合能将大于其净质量，使得如下质子衰变过程

(8)#\[\begin{equation} p \to e^+ + H \end{equation}\]

电子将被束缚在氢原子内！

以三个基本常数为轴，沿着不同方向构成了人类历史不同阶段所研究的不同理论。而我们这门课将进入右下角的世界。

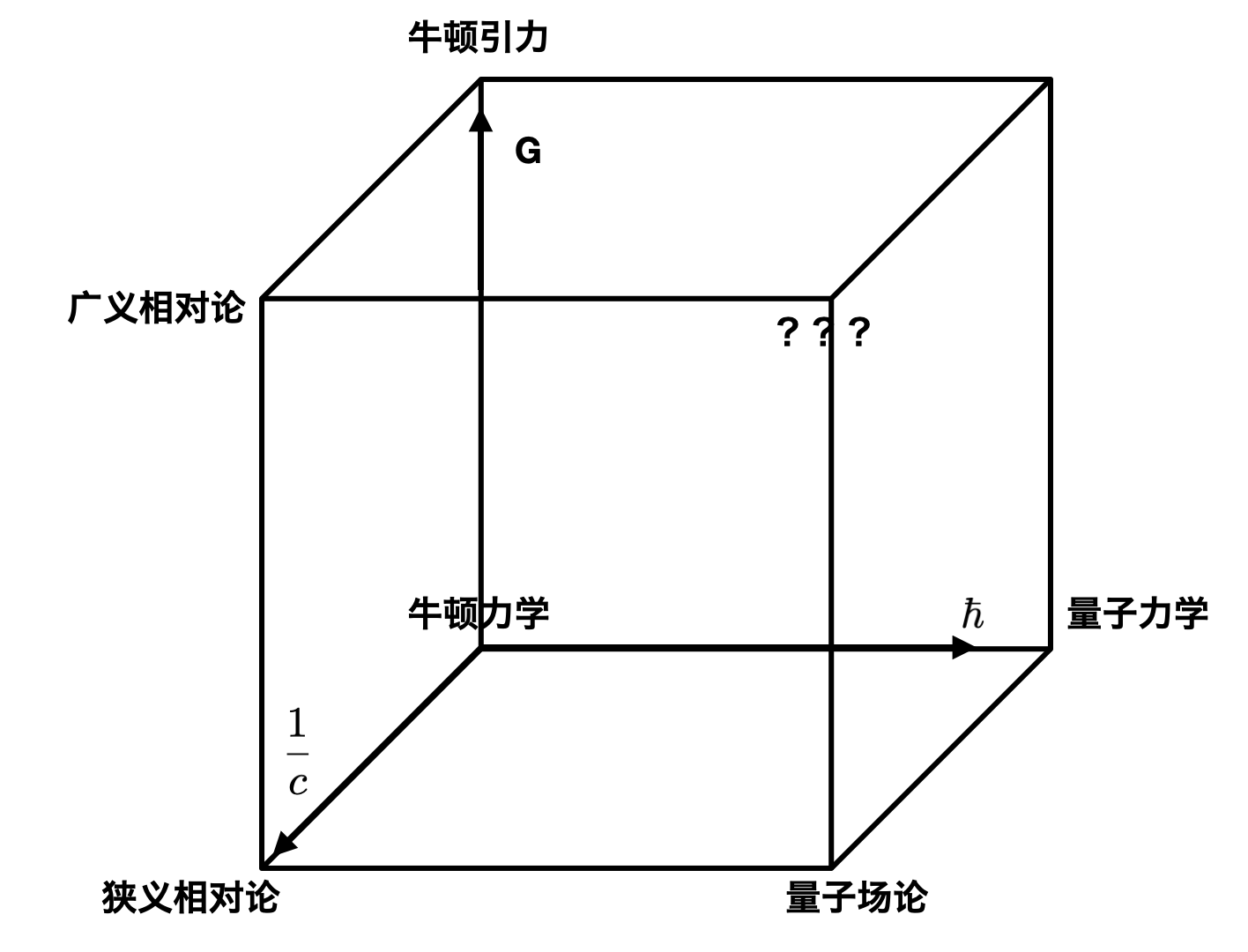
_images/theory_box.png

Fig. 3 由三个基本常数所定义的不同有效理论#

自然单位制#

由于我们将主要讨论相对论性的量子现象，如无特殊说明，我们将采用粒子物理学家的自然单位制。在自然单位制下，

(9)#\[\begin{equation} c = \hbar = 1 \end{equation}\]

在自然单位制下，所有带量纲常数（在不考虑统计力学量的情况下）均可用质量量纲表示。例如：

(10)#\[\begin{gather} [E] = [Mc^2] = [M]\\ [P] = \left[ \frac{Mv}{\sqrt{1 - v^2/c^2}}\right] = [M]\\ [\text{Length}] = [\hbar/P] = [M^{-1}]\\ [\text{time}] = [\hbar/E] = [M^{-1}] \end{gather}\]

牛顿引力常数：

(11)#\[\begin{equation} [G] = \left[V L M^{-2}\right] = [M M^{-1} M^{-2}] = [M^{-2}] \end{equation}\]

其中\(V\)是势能，\(L\)是长度。

习惯上我们以电子伏特（eV）作为能量（质量）单位，则一些典型的物理量可以表示为：

(12)#\[\begin{align} & m_\text{electron} = 5.11 \times 10^5 \text{eV} = 511 \text{KeV} = 0.511 \text{MeV} \\ &m_\text{proton} = 9.383 \times 10^8 \text{eV} = 938.3 \text{MeV} = 0.9383 \text{GeV} \\ &m_\text{neutron} = 9.395 \times 10^8 \text{eV} = 939.5 \text{MeV} = 0.9395 \text{GeV} \\ &m_\text{pion} = 1.395 \times 10^8 \text{eV} = 139.5 \text{MeV} = 0.1395 \text{GeV} \\ &m_\text{top} = 1.73 \times 10^{11} \text{eV} = 173 \text{GeV} \\ &m_\text{Higgs} = 1.25 \times 10^{11} \text{eV} = 125 \text{GeV} \\ &m_\text{sun} = 1.12 \times 10^{66} \text{eV} \\ &m_\text{Planck} = \sqrt{\frac{\hbar c}{G}} = 1.22 \times 10^{19} \text{GeV} \end{align}\]

自然单位制下的真空介电常数和真空磁导率为：

(13)#\[\begin{equation} \epsilon_0 = \mu_0 = 1 \end{equation}\]

量子电动力学中的精细结构常数为：

(14)#\[\begin{equation} \alpha = \frac{e^2}{4\pi \epsilon_0 \hbar c} \simeq \frac{1}{137} \end{equation}\]

其中\(e\)为电子电荷。

狭义相对论约定#

四维逆变矢量：

(15)#\[\begin{align} x^\mu = (t, \vec{x}) = (x^0, x^1, x^2, x^3) \\ p^\mu = (E, \vec{p}) = (p^0, p^1, p^2, p^3) \end{align}\]

\(x\)和\(y\)两点间的洛伦兹不变间隔（应用爱因斯坦求和约定）：

(16)#\[\begin{equation} \Delta s^2 = \eta_{\mu\nu} (x - y)^\mu (x - y)^\nu = (x^0 - y^0 )^2 - (\vec{x} - \vec{y})^2 \end{equation}\]

其中\(\eta_{\mu\nu}\)为闵氏空间中的度规张量：

(17)#\[\begin{equation} \eta_{\mu\nu} = \text{diag}(1, -1, -1, -1) \end{equation}\]

在这个度规约定下，

(18)#\[\begin{equation} \Delta s^2 = \left\{ \begin{array}{ll} > 0 & \text{time-like，类时间隔} \\ = 0 & \text{light-like，类光间隔} \\ < 0 & \text{space-like，类空间隔} \end{array} \right. \end{equation}\]

闵氏空间度规的逆定义为：

(19)#\[\begin{equation} \eta_{\mu\nu} \eta^{\nu \rho} = \delta_\mu^\rho \end{equation}\]

其中\(\delta^\rho_\mu\)是克朗内克符号。 可以验证：

(20)#\[\begin{equation} \eta^{\mu\nu} = \text{diag}(1, -1, -1, -1) \end{equation}\]

利用度规张量可以实现洛伦兹指标升降：

(21)#\[\begin{equation} x_\mu = \eta_{\mu\nu} x^\nu = (x^0, -x^1, -x^2, -x^3) = (x_0, x_1, x_2, x_3) \end{equation}\]

其中\(x_\mu\)称为协变矢量。

洛伦兹变换定义为保间隔不变的坐标变换：

(22)#\[\begin{equation} x^\mu \mapsto x'^\mu = \Lambda^\mu_{\ \ \nu} x^\nu \end{equation}\]

其中\(\Lambda^\mu_{\ \ \nu}\)为洛伦兹变换矩阵，它的逆记为\((\Lambda^{-1})^\mu_{\ \ \nu} := \Lambda_\nu^{\ \ \mu}\)，满足\(\Lambda^\mu_{\ \ \rho} \Lambda_\mu^{\ \ \sigma} = \delta^\sigma_\rho\)。

作业

证明：

\[\begin{equation*} \Lambda_\nu^{\ \ \mu} = \eta_{\nu\rho} \Lambda^{\rho}_{\ \ \sigma} \eta^{\sigma\mu} \end{equation*}\]

由间隔不变的定义：

(23)#\[\begin{equation} x^2 = \eta_{\mu\nu} x^\mu x^\nu \mapsto \eta_{\mu\nu} x'^\mu x'^\nu = \eta_{\mu\nu} \Lambda^\mu_{\ \ \rho} \Lambda^\nu_{\ \ \sigma} x^\rho x^\sigma = \eta_{\rho\sigma} x^\rho x^\sigma \end{equation}\]

得到洛伦兹变换矩阵定义式：

(24)#\[\begin{equation} \boxed{\eta_{\mu\nu} \Lambda^\mu_{\ \ \rho} \Lambda^\nu_{\ \ \sigma} = \eta_{\rho\sigma}} \end{equation}\]

同时间隔不变也给出逆变矢量在洛伦兹变换下的变换规则：

(25)#\[\begin{equation} x_\mu \mapsto x'_\mu = \Lambda_\mu^{\ \ \nu} x_\nu \end{equation}\]

对洛伦兹变换矩阵定义式两边乘以\(\Lambda_{\alpha}^{\ \ \rho} \Lambda_{\beta}^{\ \ \sigma}\)，得到：

(26)#\[\begin{equation} \boxed{\eta_{\alpha\beta} = \Lambda_{\alpha}^{\ \ \rho} \Lambda_{\beta}^{\ \ \sigma} \eta_{\rho\sigma}} \end{equation}\]

因此，闵氏度规是洛伦兹不变张量。

两个洛伦兹矢量的内积记为：

(27)#\[\begin{equation} a \cdot b = a^\mu b_\mu = a_\mu b^\mu \end{equation}\]

四维导数：

(28)#\[\begin{equation} \partial_\mu = \frac{\partial}{\partial x^\mu} = \left(\frac{\partial}{\partial t}, \nabla\right) \end{equation}\]

其中\(\nabla\)为三维梯度算符。

(29)#\[\begin{equation} \partial^\mu = \frac{\partial}{\partial x_\mu} = \left(\frac{\partial}{\partial t}, -\nabla\right) \end{equation}\]

四维导数的洛伦兹变换规则：

(30)#\[\begin{equation} \partial_\mu \mapsto \partial'_\mu = \frac{\partial}{\partial x'^\mu} = \Lambda_\mu^{\ \ \nu} \frac{\partial}{\partial x^\nu} = \Lambda_\mu^{\ \ \nu} \partial_\nu \end{equation}\]

因此，四维导数也是洛伦兹矢量。四维达朗伯算符写为

(31)#\[\begin{equation} \Box = \partial_\mu \partial^\mu = \frac{\partial^2}{\partial t^2} - \nabla^2 \end{equation}\]

四维Levi-Civita张量记为

(32)#\[\begin{equation} \epsilon^{\mu\nu\rho\sigma} = \left\{ \begin{array}{ll} 1 & \text{(0,1,2,3)的偶排列} \\ -1 & \text{(0,1,2,3)的奇排列} \\ 0 & \text{其它} \end{array} \right. \end{equation}\]

作业

  • 证明：

\[\begin{equation*} \Lambda^\mu_{\ \ \alpha} \Lambda^\nu_{\ \ \beta} \Lambda^\rho_{\ \ \gamma} \Lambda^\sigma_{\ \ \delta} \epsilon^{\alpha\beta\gamma\delta} = \det(\Lambda) \epsilon^{\mu\nu\rho\sigma} \end{equation*}\]

其中\(\det(\Lambda)\)为洛伦兹变换矩阵的行列式。我们将主要关心的是与单位变换连通的\(\det(\Lambda) = 1\)的情形。

狭义相对论的一个核心假设是信号传递速度是有限的。光子正好是以这个极限速度运动的粒子。所有信号传递的速度必须小于等于光速。对于相速度，由于它不传递信号，因此是可以超光速的。下面三个动画展示了相速度小于、等于、大于光速的三种情形。

相对论性量子力学与因果律破坏#

既然要讨论相对论性量子力学效应，一个自然想法是将薛定谔方程推广到相对论性的情形。薛定谔方程可以写为

(33)#\[\begin{equation} i \frac{\partial}{\partial t} |\psi(t) \rangle = H |\psi(t)\rangle \end{equation}\]

因此态矢随时间演化通过哈密顿量决定：

(34)#\[\begin{equation} |\psi(t)\rangle = e^{-iHt} |\psi(0)\rangle \end{equation}\]

在非相对论力学中，自由粒子哈密顿量可以通过动量算符写为

(35)#\[\begin{equation} H = \frac{\boldsymbol{p}^2}{2m} \end{equation}\]

一个平庸的相对论性推广是将\(H\)写为

(36)#\[\begin{equation} H = + \sqrt{\boldsymbol{p}^2 + m^2} \end{equation}\]

在取根号的时候，另一种选择是取负根，但这时就会碰到所谓的负能态问题。没有太多理由，我们这里很简单地取正根来回避这个问题。虽然哈密顿量被人为写成了正能、与相对论性质能关系相符的形式，但求解这个薛定谔方程出现所谓的因果律破坏疑难。

因果律是狭义相对论的一个重要部分。对于类空间隔的两个事件\(O_1\)和\(O_2\)，满足\((\boldsymbol{x}_1 - \boldsymbol{x}_2)^2 > t^2\)，因此即使是光信号也无法在两个事件之间传递信息。类空间隔可以用如下图的闵氏时空图示意：

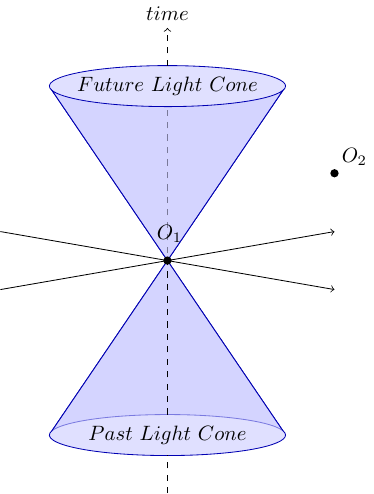
_images/lightcone.png

设想在\(T=0\)时刻，一个粒子位于\(\boldsymbol{x} = 0\)：

(37)#\[\begin{equation} |\psi(0)\rangle = | \boldsymbol{x} = 0 \rangle \end{equation}\]

在\(t\)时刻，我们问这个粒子是否能到达其自身在零时刻的光锥之外。这可通过计算粒子从\(\boldsymbol{x} = 0\)到\(\boldsymbol{x} = \boldsymbol{r}\)的概率幅来判断：

(38)#\[\begin{equation} {\cal A} = \langle \boldsymbol{r} |\psi(t) \rangle = \langle \boldsymbol{r} | e^{-i H t} |\psi(0)\rangle \end{equation}\]

其中\(|\boldsymbol{r}\rangle\)是位置本征态。我们可以将\(|\boldsymbol{r}\rangle\)展开为动量本征态的叠加：

(39)#\[\begin{equation} |\boldsymbol{r}\rangle = \int d^3 p \langle \boldsymbol{r} | \boldsymbol{p} \rangle |\boldsymbol{r} \rangle = \int \frac{d^3 p}{(2\pi)^{3/2}} e^{i \boldsymbol{p} \cdot \boldsymbol{r}} |\boldsymbol{p}\rangle \end{equation}\]

代入概率幅公式中，得到

(40)#\[\begin{equation} {\cal A} = \int \frac{d^3 p}{(2\pi)^3} e^{i \boldsymbol{p} \cdot \boldsymbol{r}} e^{-i \omega_p t} \end{equation}\]

其中

(41)#\[\begin{equation} \omega_p = \sqrt{\boldsymbol{p}^2 + m^2} \end{equation}\]

在球极坐标下，令\(\boldsymbol{p} \cdot \boldsymbol{r} = p r \cos\theta\)，

(42)#\[\begin{align} {\cal A} &= \int_0^\infty \frac{p^2 dp}{(2\pi)^3} \int_{-1}^1 d \cos\theta \int_0^{2\pi} d\phi \ e^{i p r \cos\theta} e^{-i \omega_p t} \\ &= \int_0^\infty \frac{p^2 dp}{(2 \pi)^2} \frac{1}{ipr} \left( e^{i p r} - e^{-i p r} \right) e^{-i \omega_p t} \\ &= \int_{-\infty}^{\infty} \frac{p dp}{(2 \pi)^2} \frac{1}{ir} e^{ipr} e^{-i \sqrt{\boldsymbol{p}^2 + m^2} t} \end{align}\]

们来看质量非零的情况。事实上，上面定义的振幅应该视作一个分布。对于一个分布，我们可以引入一个正规化参数使其成为一个普通函数。这里，我们可以让\(t \to t - i \epsilon\)，其中\(\epsilon\)是一个正实数，在\(\epsilon \to 0\)的极限下过渡到对应的分布。这时概率幅写为

(43)#\[\begin{equation} {\cal A} = \int_{-\infty}^{\infty} \frac{p dp}{(2 \pi)^2} \frac{1}{ir} e^{i p r} e^{-i \sqrt{\boldsymbol{p}^2 + m^2} t - \epsilon \sqrt{\boldsymbol{p}^2 + m^2}} \end{equation}\]

将\(p\)解析延拓到整个复平面，被积函数具有形式

(44)#\[\begin{equation} F(p) e^{ipr - i \sqrt{p^2 + m^2} t} \end{equation}\]

\(\lim_{p \to \pm \infty}F(p) = \lim_{p \to \pm \infty} p e^{-\epsilon \sqrt{p^2 + m^2}} \to 0\)。借助复变函数中的约当引理，可以将对\(p\)的积分解析延拓到上半平面，并忽略大圆弧的贡献，仅留下沿割线两岸的贡献，如下图所示。

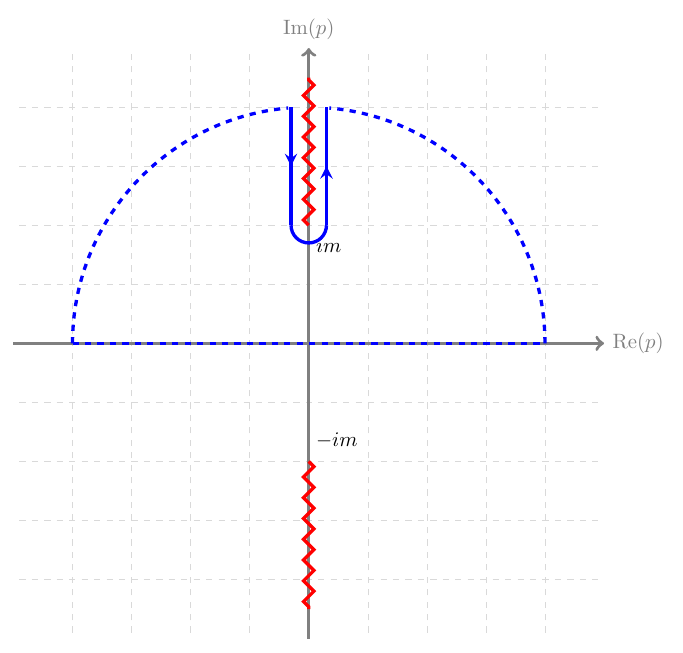
_images/contour_naive.png

沿着割线两岸的积分可以写作：

(45)#\[\begin{equation} {\cal A} = \frac{i}{(2 \pi)^2 r} \int_m^\infty z dz\ e^{-zr} \Big[ e^{t \sqrt{z^2 - m^2}} - e^{- t \sqrt{z^2 - m^2}} \Big] \end{equation}\]

注意到对任何\(r>t\)，即在光锥之外，被积函数是正定的，因此积分结果也必然非零。这告诉我们对哈密顿量所作的简单相对论性修改无法满足因果律的要求，必须引入新的理论形式。

上面积分的计算过程中引入\(t - i \epsilon\)的过程也许会让人困惑。为了更好看清这个手续是合法的，我们引用这个积分的封闭解：

(46)#\[\begin{equation} {\cal A} = \frac{m^2}{2 \pi^2} \frac{t}{i \tau^2} K_2(i m \tau) \end{equation}\]

其中

(47)#\[\begin{equation} \tau = \lim_{\epsilon \to 0_+} \sqrt{(t - i \epsilon)^2 - r^2} \end{equation}\]

\(K_2(z)\)是第二类贝塞尔函数。在\(\tau = 0\)，即在光锥上，这个结果必须解释成分布，而在光锥之外，它的行为是良定义函数。我们关心的主要是类空间隔的信号传播，在这个区域\(\epsilon \to 0\)的极限是光滑的。[1]

洛伦兹变换和洛伦兹群#

请参考： Lorentz Transformation by Robert G. Littlejohn