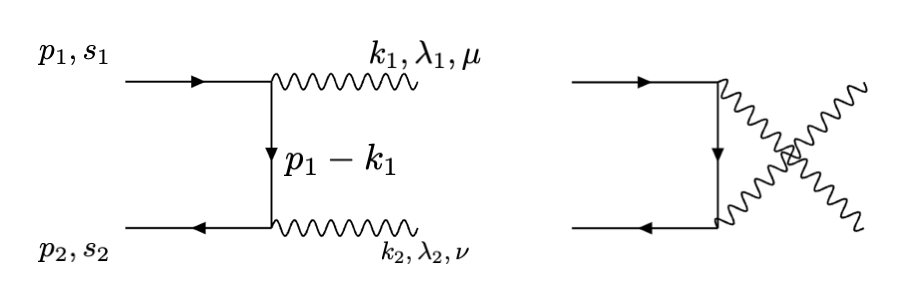矢量场与物质相互作用

在讨论完自由无质量矢量场的量子化后，我们现在来讨论矢量场与物质的相互作用。按照之前的原则，我们将仅讨论相互作用项的算符量纲小于等于四的情况。由于实标量场不带有内部对称性，而光子仅与带电物质相互作用，因此我们这里忽略掉实标量场。

复标量场 （标量电动力学）

我们之前已经知道，复标量场具有\(U(1)\)整体内部对称性，因此可以携带内部荷。如果要写下复标量和光子的相互作用拉氏量，在考虑洛伦兹对称性和量纲约束的前提下，只有如下几种选项：

(851)\[\begin{equation} A_\mu (\partial^\mu \Phi^\dagger) \Phi + A_\mu \Phi^\dagger (\partial^\mu \Phi), \quad A_\mu A^\mu \Phi^\dagger \Phi \end{equation}\]

这两个算符量纲均为四，因此其耦合常数应是无量纲的。不失一般性，我们假设拉氏量写为

(852)\[\begin{equation} {\cal L} = \partial \Phi^\dagger \partial^\mu \Phi - m^2 \Phi^\dagger \Phi - \frac{1}{4} F_{\mu \nu}F^{\mu \nu} + a A_\mu (\partial^\mu \Phi^\dagger) \Phi + b A_\mu \Phi^\dagger (\partial^\mu \Phi) + c A_\mu A^\mu \Phi^\dagger \Phi \end{equation}\]

我们注意到，这个拉氏量仍然具有整体的\(U(1)\)内部对称性：

(853)\[\begin{equation} \Phi(x) \to e^{i\beta} \Phi(x) \end{equation}\]

但在定域规范变换下

(854)\[\begin{equation} A_\mu(x) \to A_\mu(x) + \partial_\mu \alpha(x) \end{equation}\]

拉氏量变为：

(855)\[\begin{equation} {\cal L} \overset{\alpha(x)}{\to} {\cal L} + a (\partial_\mu \alpha(x)) (\partial^\mu \Phi^\dagger) \Phi + b (\partial_\mu \alpha(x)) \Phi^\dagger (\partial^\mu \Phi) + 2 c (\partial_\mu \alpha(x)) A^\mu \Phi^\dagger \Phi + c (\partial_\mu \alpha(x)) (\partial^\mu \alpha(x)) \Phi^\dagger \Phi \end{equation}\]

但规范对称性的存在是使得光子场的自由度与物理自由度个数一致，我们无法接受规范对称性被破坏。我们尝试提升标量场的整体对称性为定域对称性，\(\beta \to \beta(x)\)，这时在矢量场的规范变换和标量场的定域规范变换联合作用下，拉氏量额外产生的项为：

(856)\[\begin{align} {\cal L} \overset{\alpha(x), \beta(x)}{\to} &\ {\cal L} + i (\partial_\mu \beta(x)) [ (\partial^\mu \Phi^\dagger) \Phi - \Phi^\dagger (\partial^\mu \Phi) ] + (\partial_\mu \beta(x)) (\partial^\mu \beta(x)) \Phi^\dagger \Phi + i (-a + b)(\partial_\mu \beta(x)) A^\mu \Phi^\dagger \Phi \\ &\ + a (\partial_\mu \alpha(x)) (\partial^\mu \Phi^\dagger) \Phi + b (\partial_\mu \alpha(x)) \Phi^\dagger (\partial^\mu \Phi) + 2 c e (\partial_\mu \alpha(x)) A^\mu \Phi^\dagger \Phi + c (\partial_\mu \alpha(x)) (\partial^\mu \alpha(x)) \Phi^\dagger \Phi \\ + &\ i (-a + b)(\partial_\mu \beta(x)) (\partial^\mu \alpha(x) )\Phi^\dagger \Phi \end{align}\]

我们发现，如果让

(857)\[\begin{equation} c= 1 \,, \qquad a = -i \,, \qquad b = i \,, \qquad \beta(x) = \alpha(x) \end{equation}\]

则此时的拉氏量

(858)\[\begin{equation} {\cal L} = \partial \Phi^\dagger \partial^\mu \Phi - m^2 \Phi^\dagger \Phi - \frac{1}{4} F_{\mu \nu}F^{\mu \nu} - i A_\mu (\partial^\mu \Phi^\dagger) \Phi + i A_\mu \Phi^\dagger (\partial^\mu \Phi) + A_\mu A^\mu \Phi^\dagger \Phi \end{equation}\]

在联合定域规范变换

(859)\[\begin{equation} \Phi(x) \to e^{i\alpha(x)} \Phi(x) \,, \qquad A_\mu(x) \to A_\mu(x) + \partial_\mu \alpha(x) \end{equation}\]

仍然是不变的。这就给出了既不破坏光子场的规范不变性从而保证矢量场自由度个数与物理自由度个数一致，同时又能引入光子与物理相互作用的要求。我们将这个拉氏量称为标量电动力学的拉氏量。

极小耦合

事实上，上述的拉氏量可以通过一个更加一般的方法得到。我们考虑一个自由复标量场与一个自由无质量矢量场的相叠加，其拉氏量为

(860)\[\begin{equation} {\cal L} = \partial \Phi^\dagger \partial^\mu \Phi - m^2 \Phi^\dagger \Phi - \frac{1}{4} F_{\mu \nu}F^{\mu \nu} \end{equation}\]

然后我们将对物质场的导数提升为协变倒数：

(861)\[\begin{equation} \partial_\mu \to D_\mu = \partial_\mu + i e A_\mu \end{equation}\]

这里我们还额外引入了一个电荷单位\(e\)。我们发现在如下联合定域规范变换下：

(862)\[\begin{equation} \Phi(x) \to e^{ - i e \alpha(x)} \Phi(x) \,, \qquad A_\mu(x) \to A_\mu(x) + \partial_\mu \alpha(x) \end{equation}\]

有

(863)\[\begin{equation} D_\mu \Phi(x) \to e^{ - i e \alpha(x)} D_\mu \Phi(x) \end{equation}\]

因此拉氏量

(864)\[\begin{equation} {\cal L} = (D_\mu \Phi)^\dagger (D^\mu \Phi) - m^2 \Phi^\dagger \Phi - \frac{1}{4} F_{\mu \nu}F^{\mu \nu} \end{equation}\]

是显式规范不变的，同时也包含了光与物质间的相互作用。这种形式的光与物质相互作用称为极小耦合。

量子电动力学 （QED）

有了标量电动力学的例子，我们可以立刻通过极小耦合的形式引入光与费米子间的相互作用：

(865)\[\begin{equation} {\cal L} = \bar{\psi} (i \gamma^\mu D_\mu - m) \psi - \frac{1}{4} F_{\mu \nu}F^{\mu \nu} \end{equation}\]

这里\(D_\mu\)是协变导数：

(866)\[\begin{equation} D_\mu = \partial_\mu + i e A_\mu \end{equation}\]

这个拉氏量所定义的理论称作量子电动力学，它在如下联合规范变换下是不变的：

(867)\[\begin{equation} \psi(x) \to e^{ - i e \alpha(x)} \psi(x) \,, \qquad A_\mu(x) \to A_\mu(x) + \partial_\mu \alpha(x) \end{equation}\]

QED费曼规则

显然，QED中费米子和光子的传播子自由理论的传播子相同，而相互作用拉氏量仅有一项：

(868)\[\begin{equation} {\cal L}_{\rm int} = - e \bar{\psi} \gamma^\mu \psi A_\mu \end{equation}\]

为了得到相应的费曼规则，我们考虑三点连通关联函数：

(869)\[\begin{equation} \langle 0 | T \{ \psi(x_1) \bar{\psi}(x_2) A_\mu(x_3) e^{-i \int d^4 w \, {\cal H}_I(w)}\} | 0 \rangle \end{equation}\]

其中

(870)\[\begin{equation} {\cal H}_I(w) = e \bar{\psi} \gamma^\mu \psi A_\mu(w) \end{equation}\]

展开到\(e\)的第一阶，我们有

(871)\[\begin{align} &\ -i e \langle 0 | T \{ \psi_\beta(x_1) \bar{\psi}_\alpha(x_2) A_\mu(x_3) \int d^4 w \, \bar{\psi}_\delta(w) \gamma^\nu_{\delta \sigma} \psi_\sigma(w) A_\nu(w) \} | 0 \rangle \\ =&\ -i e \gamma^\nu_{\delta \sigma} \int d^4 w \, \Delta_{\beta\delta}(x_1 - w) \Delta_{\sigma\alpha}(w- x_2) \Delta_{\mu\nu}(x_3 - w) \end{align}\]

其中

(872)\[\begin{equation} \Delta_{\mu\nu}(x) = \int \frac{d^4 k}{(2\pi)^4} \frac{-i g_{\mu\nu}}{k^2 + i \epsilon} e^{-i k \cdot x} \end{equation}\]

(873)\[\begin{equation} \Delta_{\alpha\beta}(x) = \int \frac{d^4 k}{(2\pi)^4} \frac{i (\gamma^\mu k_\mu + m)_{\alpha\beta}}{k^2 - m^2 + i \epsilon} e^{-i k \cdot x} \end{equation}\]

我们立刻读出动量空间的电子和光子相互作用费曼规则为：

(874)\[\begin{equation} - i e \gamma^\nu \end{equation}\]

此外，对于每一个动量为\(k\)，极化为\(\lambda\)的入射光子，我们乘上\(\epsilon_\mu^*(k, \lambda)\)，对于每一个动量为\(k\)，极化为\(\lambda\)的出射光子，我们乘上\(\epsilon_\mu(k, \lambda)\)。

QED的树图散射振幅的简单例子

以\(e^+e^-\)湮灭到一对光子为例，这个过程的动量记为

(875)\[\begin{equation} e^-(p_1) + e^+(p_2) \to \gamma(k_1) + \gamma(k_2) \end{equation}\]

相应的费曼图为：

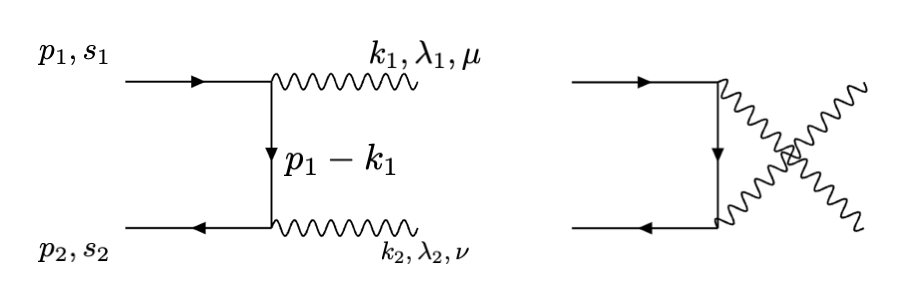
将费曼规则代入，得到

(876)\[\begin{align} iM = &\ \bar v_{s_2} (p_2) (-ie \gamma_\nu) \frac{i ({p\!\!\!\big /}_1 + {k\!\!\!\big /}_1 ) +m}{(p_1-k_1)^2 - m^2} (-ie\gamma_\mu) u_{s_1} (p_1) \epsilon^\mu (k, \lambda_1) \epsilon^\nu (k_2, \lambda_2) \\ &\ + \bar v_{s_2} (p_2) (-ie \gamma_\nu) \frac{i ({p\!\!\!\big /}_1 - {k\!\!\!\big /}_2 ) +m}{(p_1-k_2)^2 - m^2} ( -ie \gamma_\mu) u_{s_1} (p_1) \epsilon^\mu (k, \lambda_1) \epsilon^\nu (k_2, \lambda_2) \end{align}\]