如果大家还记得的话,在我们讨论QED电磁形状因子的单圈修正时,在紫外发散之外外碰到了红外发散。我们当时处理的方式是给光子一个小的质量从而使得积分收敛。这一章我们尝试更系统的讨论红外发散的问题。
首先,为什么我们之前的计算会出现红外发散?从概念层面来说,这是因为我们之前的计算问了一个不恰当的问题(用现代的术语来说,问了一个红外不安全的问题。)。例如,在讨论\(e^+ \mu^+ \to e^+ \mu^+\)的单圈图修正之时,我们问的问题是末态观测到一个电子和一个谬子的概率。但这个问题在实验上无法精确定义。原因是由于探测器所具有的内禀误差,我们无法精确排除额外辐射一个软光子的过程。这里软光子指的是能量很低的光子。
更一般的,由于红外发散的存在,具有无质量规范玻色子的规范理论的散射振幅至今也没有良好定义(当然文献上存在这方面的努力,例如Faddeev-Kulish形式)。只有概率水平的观测量才是良好定义的。
软光子定理
首先我们考虑一个一般的QED过程,其中包含一定数目的入射或出射电子或正电子,以及一个额外的光子。我们关心当光子能量趋于零时振幅的极限行为。例如,考虑从一个末态电子辐射一个光子的费曼图:
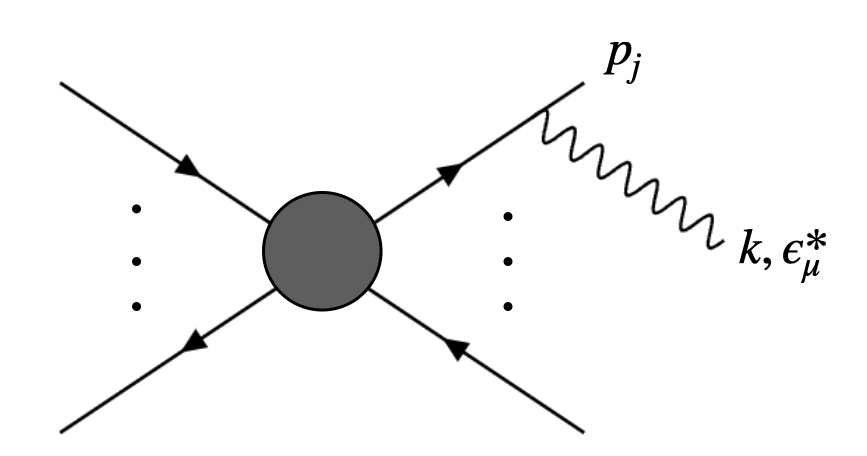
这个费曼图对应的振幅可以写为
(993)\[\begin{equation}
M_i(\{p\}_n, k) = \bar u(p_j) (-ie \gamma^\mu) \epsilon_\mu^*(k, \lambda)
\frac{i (p_j\!\!\!\!\! \big / + k\!\!\! \big / + m)}{(p_j + k)^2 - m^2 + i \epsilon} \overline{M}
\end{equation}\]
其中\(\overline{M}\)是去掉\(p_j\)和\(k\)的其余费曼图的振幅。我们注意到,当\(k \to 0\)时,传播子的极限行为为
(994)\[\begin{equation}
\bar u(p_j) (-ie \gamma^\mu) \frac{i (p_j\!\!\!\!\! \big / + k\!\!\! \big / + m)}{(p_j + k)^2 - m^2 + i \epsilon} \to \bar u(p_j) (-ie \gamma^\mu) \frac{i (p_j\!\!\!\!\! \big / + m)}{2 p_j \cdot k + i \epsilon}
\end{equation}\]
利用狄拉克矩阵的性质,
(995)\[\begin{align}
\bar{u}(p_j) (-ie \gamma^\mu) (p_j\!\!\!\!\! \big / + m) &= (-ie) \bar{u}(p_j) \left[ - p_j\!\!\!\!\! \big / \gamma^\mu + 2 p_j^\mu + m \gamma^\mu \right] \\
&= (-ie) \bar{u}(p_j) 2 p_j^\mu \\
\end{align}\]
在上式我们应用了狄拉克方程。因此这个费曼图的领头贡献可以写为
(996)\[\begin{equation}
M_i(\{p\}_n, k) \to \frac{e p_j^\mu \epsilon_\mu^*(k,\lambda)}{2 p_j \cdot k + i \epsilon} M(\{p\}_n)
\end{equation}\]
其中\(M(\{p\}_n)\)是去掉光子后的散射振幅。我们注意到,这个费曼图在光子能量趋于零时是发散的,体现为分母上的\(k\)依赖。
类似的,还可以讨论光子从外线的出射正电子,入射电子,及入射正电子辐射的行为。它们均具有类似的红外奇异行为。而当光子从内线辐射时,由于内线动量通常不在壳,因此光子的零动量极限是一个光滑极限。综上,我们得到如下定理(温伯格软光子定理):在QED中,从一个一般的带电粒子散射过程中辐射一个软光子的振幅在零动量极限下可以写为:
(997)\[\begin{equation}
M_i(\{p\}_n, k) \to \sum_{j} \frac{e \eta_j p_j^\mu \epsilon_\mu^*(k,\lambda)}{2 p_j \cdot k + \sigma_j i \epsilon} M(\{p\}_n)
\end{equation}\]
其中求和遍历所有外线粒子。对于出射电子和入射正电子,\(\eta_j = 1\),对于入射电子和出射正电子,\(\eta_j = -1\)。对于入射粒子,\(\sigma_j = -1\),对于出射粒子,\(\sigma_j = 1\)。
利用这个结果,我们可以精确验证之前关于红外安全性质的论断。
红外发散的相消
我们在这一节讨论红外发散如何在虚修正和实修正间相消的。
我们考虑如下过程:
(998)\[\begin{equation}
\gamma^* (q) \to e^-(p_1) + e^+(p_2)
\end{equation}\]
及其虚和实修正,其中\(\gamma^*\)是一个离壳光子。
为了简单起见,我们仅讨论一阶修正的情形。
一阶实辐射修正
首先考虑一阶实辐射修正:
(999)\[\begin{equation}
\gamma^* (q) \to e^-(p_1) + e^+(p_2) + \gamma(k)
\end{equation}\]
在\(k^\mu \to 0\)时,这个过程的振幅可以写为
(1000)\[\begin{equation}
M_{\gamma^* \to e^-e^+ \gamma} = M_{\gamma^* \to e^-e^+} \left(
\frac{p_1 \cdot \epsilon^*(k, \lambda)}{p_1 \cdot k} - \frac{p_2 \cdot \epsilon^*(k, \lambda)}{p_2 \cdot k}
\right)
\end{equation}\]
其中\(M_{\gamma^* \to e^-e^+}\)是去掉光子的散射振幅。对振幅求模方,并利用\(\sum_\lambda \epsilon_\mu^*(k, \lambda) \epsilon_\nu(k,\lambda) = - \eta_{\mu\nu}\)对极化光子极化矢量求和,得到
(1001)\[\begin{equation}
|M_{\gamma^* \to e^-e^+ \gamma}|^2 = |M_{\gamma^* \to e^-e^+}|^2 e^2 \left(
- \frac{p_1^2}{(p_1 \cdot k)^2} - \frac{p_2^2}{(p_2 \cdot k)^2} + 2 \frac{p_1 \cdot p_2}{(p_1 \cdot k) (p_2 \cdot k)}
\right)
\end{equation}\]
其中\(p_1^2 = p_2^2 = m^2\)。
在软极限下,软光子的相空间可以近似写为
(1002)\[\begin{equation}
\int \frac{d^3 k}{(2\pi)^3 2 k^0}
\end{equation}\]
因此实辐射概率可以写为
(1003)\[\begin{equation}
d\sigma_{\text{real}} = d\sigma_{\gamma^* \to e^-e^+} \times {\cal K_R}
\end{equation}\]
其中
(1004)\[\begin{equation}
{\cal K_R} = e^2 \int \frac{d^3 k}{(2\pi)^3 2 k^0} \left(
- \frac{p_1^2}{(p_1 \cdot k)^2} - \frac{p_2^2}{(p_2 \cdot k)^2} + 2 \frac{p_1 \cdot p_2}{(p_1 \cdot k) (p_2 \cdot k)}
\right)
\end{equation}\]
将动量作如下参数化:
(1005)\[\begin{equation}
p_1^\mu = m v_1^\mu \,, \qquad p_2^\mu = m v_2^\mu\,, \qquad v_1^2 = v_2^2 = 1
\end{equation}\]
在\(q\)的质心系,将\(v_1\)和\(v_2\)参数化为
(1006)\[\begin{equation}
v_1 = \frac{1}{\sqrt{1 - \beta^2}} (1 , 0, 0, \beta ) \,, \qquad
v_2 = \frac{1}{\sqrt{1 - \beta^2}} (1 , 0, 0, -\beta )
\end{equation}\]
其中\(\beta = \sqrt{1 - 4 m^2/q^2}\)。此时我们的积分写为
(1007)\[\begin{equation}
{\cal K}_R = e^2 \int_{\omega}^{\Lambda} \frac{d k^0}{ (2 \pi)^3 2 k^0}
\int d \Omega_{\hat k} \left(
- \frac{1}{v_1 \cdot \hat k} - \frac{1}{v_2 \cdot \hat k} + 2 \frac{v_1 \cdot v_2}{(v_1 \cdot \hat k) (v_2 \cdot \hat k)}
\right)
\end{equation}\]
其中我们对光子能量积分分别引入了红外和紫外截断。红外截断引入的原因是红外发散的存在,因此可以认为是一种正规化手段。红外截断参数\(\omega\)可以认为是探测器所能达到的最低能量分辨率。角积分测度可以写为
(1008)\[\begin{equation}
d \Omega_{\hat k} = \int_0^{2 \pi} d \phi \int_{-1}^1 d \cos\theta
\end{equation}\]
其中\(\theta\)是光子动量和电子动量的夹角:
(1009)\[\begin{equation}
v_1 \cdot \hat k = 1 - \beta \cos\theta \,, \qquad v_2 \cdot \hat k = 1 + \beta \cos \theta
\end{equation}\]
在这个参数化下,最后的积分结果为
(1010)\[\begin{equation}
{\cal K}_R = \frac{\alpha}{2 \pi} \ln \frac{\Lambda}{\omega} \left( -4 + \frac{2 (1 + \beta^2)}{\beta} \ln \frac{1 + \beta}{1 - \beta} \right)
\end{equation}\]
其中
(1011)\[\begin{equation}
\alpha = \frac{e^2}{4 \pi}
\end{equation}\]
是精细结构常数。
一阶虚修正
我们现在考虑一阶虚修正。相应的费曼图为:
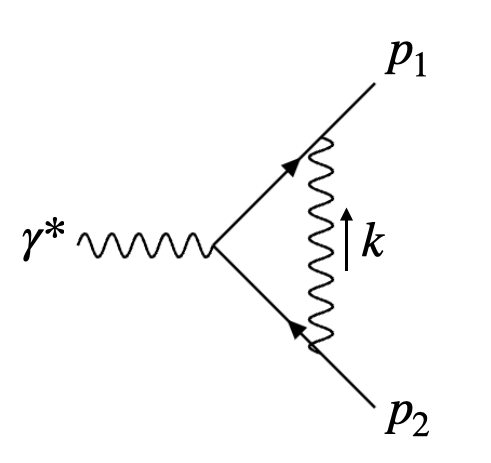
在在壳重整化方案下,外线自能被抵消项完全抵消,因此我们这里不予考虑。同样的,我们考察软光子极限下振幅的行为:
(1012)\[\begin{equation}
M^{(1)}_{\gamma^* \to e^-e^+} \simeq M^{(0)}_{\gamma^* \to e^-e^+}
{\cal K}_V
\end{equation}\]
其中
(1013)\[\begin{equation}
{\cal K}_V = \int \frac{d^4 k}{(2 \pi)^4} e^2 (-i) \left[ \frac{1}{k^2 + i \epsilon} \frac{ p_1 \cdot p_2 }{(k \cdot p_1 - i \epsilon) (k \cdot p_2 + i \epsilon)} \right]
\end{equation}\]
与实修正不一样,对于虚修正,\(i\epsilon\)是重要的,我们这里保留。对\(k^0\)积分我们可以用留数定理先积掉。
通过求解方程:
(1014)\[\begin{equation}
k^2 + i \epsilon = 0 \,, \qquad
p_1 \cdot k - i \epsilon = 0 \,, \qquad
p_2 \cdot k + i \epsilon = 0
\end{equation}\]
其中\(p_1\),\(p_2\),和\(\vec k\)的参数化与上一节一致,
可以得到传播子关于\(k^0\)的极点位置为:
(1015)\[\begin{align}
k^0 =&\ \pm |\vec k| \mp i \epsilon
\\
k^0 = &\ \cos \theta \beta | \vec k | - i \epsilon
\\
k^0 = &\ - \cos \theta \beta | \vec k | + i \epsilon
\end{align}\]
对于\(k^0\)的复平面积分,我们不妨绕上半平面无穷大半圆弧构成封闭围道。利用留数定理,对于\(k^0 = - |\vec k| + i \epsilon\)的极点,给出如下贡献
(1016)\[\begin{equation}
{\cal K}_{V,1} = e^2 (v_1 \cdot v_2) \int \frac{d^3 k}{(2 \pi)^3}
\frac{1}{- 2 | \vec k|^3} \frac{1 - \beta^2}{(1 - \beta \cos\theta) (1 + \beta \cos\theta)}
\end{equation}\]
对\(|\vec k|\)的积分引入积分引入正规化\(\omega < |\vec k|<m\),其中\(m\)是电子质量,而角度积分可以很轻易得到,结果为
(1017)\[\begin{equation}
{\cal K}_{V,1} = \frac{\alpha}{2 \pi} \frac{ (1 + \beta^2)}{\beta} \ln \frac{1 + \beta}{1 - \beta} \ln \frac{m}{\omega}
\end{equation}\]
而对于\(k^0 = - \frac{1}{\sqrt{1 - \beta^2}} \cos \theta \beta | \vec k | + i \epsilon\)的极点,给出如下贡献
(1018)\[\begin{equation}
{\cal K}_{V,2} = e^2 (v_1 \cdot v_2) \int \frac{d^3 k}{(2 \pi)^3}
\frac{1}{|\vec k|^2 \left( \cos\theta^2 \beta^2 - 1\right) + i \epsilon} \frac{1 - \beta^2}{(-2 \cos\theta \beta | \vec k| - i \epsilon)}
\end{equation}\]
类似的,对于\(\vec k|\)的积分,给出一个因子\(\ln \frac{m}{\omega}\)。而对于\(\cos\theta\)的积分可以写为
(1019)\[\begin{equation}
\frac{1-\beta^2}{- 2 \beta} \int_{-1}^1 d \cos\theta\,
\frac{1}{\cos\theta^2 \beta^2 - 1 + i \epsilon} \frac{1 }{(\cos\theta + i \epsilon)}
\end{equation}\]
利用分布恒等式:
(1020)\[\begin{equation}
\frac{1}{X + i \epsilon} = {\cal P} \frac{1}{X} - i \pi \delta(X)
\end{equation}\]
其中\({\cal P}\)代表主值积分。容易看出主值部分积分为零,而delta函数部分给出
(1021)\[\begin{equation}
- i \pi \frac{1-\beta^2}{ 2 \beta}
\end{equation}\]
这是一个纯虚的因子。在计算一阶截面修正时,我们须要求
(1022)\[\begin{equation}
M^{(1)}_V M^{(0),*} + M^{(0)} M^{(1),*}_V = 2 M^{(0)} \text{Re} M^{(1),*}_V
\end{equation}\]
因此这一阶虚部部分对截面没有贡献。
最后,我们还需考虑顶角抵消项的贡献:
(1023)\[\begin{equation}
{\cal K}_{\text{c.t.}} = M^{(0)}_{\gamma^* \to e^-e^+} (Z_1 - 1)
\end{equation}\]
在在壳重整化方案下,顶角重整化常数为
(1024)\[\begin{equation}
Z_1 = 1 = \frac{\alpha}{2 \pi} \left[ - \frac{1}{\epsilon_{\rm uv}} + 2 \ln \frac{m}{\omega} - \frac{1}{2} \ln \frac{\mu^2}{m^2} - \frac{5}{4}\right]
\end{equation}\]
其中\(\epsilon_{\rm uv} = 2 - d/2\)是紫外发散的维数正规化参数。因此,最终的虚修正贡献为(仅保留红外奇异项)
(1025)\[\begin{equation}
{\cal K}_V = \frac{\alpha}{2 \pi} \left[2 + \frac{ (1 + \beta^2)}{\beta} \ln \frac{1 + \beta}{1 - \beta} \right] \ln \frac{m}{\omega}
\end{equation}\]
一阶总截面
结合实和虚的一阶修正,我们得到最终结果(忽略掉与红外发散无关项):
(1026)\[\begin{align}
{\cal K}_{\rm tot.} =&\ {\cal K}_R + 2 {\cal K}_V
\\
=&\ \frac{\alpha}{2 \pi} \ln \frac{\Lambda}{m} \left( -4 + \frac{2 (1 + \beta^2)}{\beta} \ln \frac{1 + \beta}{1 - \beta} \right)
\end{align}\]
我们看到,在虚修正与实修正之和中,红外正规化参数\(\omega\)的依赖被完全消掉了,剩下的是有限的实因子。在高能极限,或者等价的在\(m \to 0\)的极限下,也就是\(\beta \to 1\),这个因子可以写为
(1027)\[\begin{equation}
{\cal K}_{\rm tot.} \simeq \frac{\alpha}{2 \pi} \ln \frac{\Lambda}{m} \left( -4 +4 \ln \frac{q^2}{m^2} \right)
\end{equation}\]
我们注意到领头的贡献是一个双对数项:\(\ln\frac{\Lambda}{m} \ln\frac{q^2}{m^2}\)。高能极限下出现的双对数项称作Sudakov双对数。


