两点Wightman函数
我们将实标量场写成两部分:
(242) \[\begin{equation}
\phi(x) = \phi^+(x) + \phi^-(x)
\end{equation}\]
其中
(243) \[\begin{align}
\phi^-(x) &= \int \frac{d^3 k}{(2\pi)^{3/2} \sqrt{2 \omega_k}}
a_{\boldsymbol{k}} e^{-ikx}
\\
\phi^+(x) &= \int \frac{d^3 k}{(2\pi)^{3/2} \sqrt{2 \omega_k}}
a_{\boldsymbol{k}}^\dagger e^{ikx}
\end{align}\]
\(\phi^+\) 的作用是激发出一个粒子,\(\phi^-\) 的作用是湮灭一个粒子。这时,我们未加思索得问这样一个问题,在真空中从\(y\) 点激发出一个粒子,然后在\(x\) 点湮灭这个粒子,这个过程的概率是多少?这个概率可以用两点Wightman函数来描述:
(244) \[\begin{equation}
\Delta_+(x - y) = \langle 0 | \phi(x) \phi(y) |0\rangle =
% can be written as function of \phi^- and \phi^+
\langle 0 | \phi^-(x) \phi^+(y) |0\rangle
\end{equation}\]
注意到,Wightman函数在主动的洛伦兹变换\(\Lambda\) 下变为:
(245) \[\begin{split}
\begin{align}
\Delta_+(x - y) & \to \langle 0 | U(\Lambda)^\dagger \phi^-( x) \phi^+(y) U(\Lambda)|0\rangle \\
&= \langle 0 | \phi^-( \Lambda^{-1} x) \phi^+( \Lambda^{-1} y) |0\rangle \\
&= \Delta_+(\Lambda^{-1} x - \Lambda^{-1} y)
\end{align}
\end{split}\]
稍后我们会用到这个结果。
现在回到我们最关心的问题。当\(x\) 和\(y\) 处于类空间隔时,即\((x-y)^2 < 0\) ,我们期待两点间无法进行信号传递,因此期待\(\Delta_+(x - y) = 0\) 。但果真如此吗?我们来计算一下:
(246) \[\begin{align}
\Delta_+(x - y) &= \langle 0 | \phi^-(x) \phi^+(y) |0\rangle \\
&= [\phi^-(x), \phi^+(y)] \\
&= \int \frac{d^3 k}{(2\pi)^{3/2} \sqrt{2 \omega_k}} e^{-i k\cdot x} \int \frac{d^3 k'}{(2\pi)^{3/2} \sqrt{2 \omega_{k'}}} e^{i k'\cdot y} [a_{\boldsymbol{k}}, a_{\boldsymbol{k}'}^\dagger] \\
&= \int \frac{d^3 k}{(2\pi)^{3/2} \sqrt{2 \omega_k}} e^{-i k\cdot x} \int \frac{d^3 k'}{(2\pi)^{3/2} \sqrt{2 \omega_{k'}}} e^{i k'\cdot y} \delta^{(3)}(\boldsymbol{k} - \boldsymbol{k}') \\
&= \int \frac{d^3 k}{(2\pi)^{3/2} 2 \omega_k} e^{-i k\cdot (x - y)}
\end{align}\]
这个积分与我们在相对论性量子力学中讨论的积分类似,因此计算方法不再赘述。可以证明,即使对于很大的类空间隔\((x-y)^2 \simeq - r^2 \to \infty\) ,\(\Delta_+(x - y) \simeq e^{-mr} \neq 0\) 。因此,我们面临了与相对论量子力学中同样的问题,即因果律被破坏了。
回想一下,我们从场论出发构造满足相对论原理的量子理论的原因是更容易实现
(247) \[\begin{split}
\begin{aligned}
\phi^-(x) &= \int \frac{d^3 k}{(2\pi)^{3/2} \sqrt{2 \omega_k}} a_{\boldsymbol{k}} e^{-ikx} \\
&= i \int \frac{d^3 k}{(2\pi)^{3/2} \sqrt{2 \omega_k}}\int \frac{d^3 x}{(2\pi)^{3/2}} \frac{1}{\sqrt{2 \omega_k}} e^{i \boldsymbol{k} \cdot (\boldsymbol{x}' - \boldsymbol{x})} ( \dot \phi(x) - i \omega_k \phi(x))\\
&= \frac{1}{2} \phi(x) + i \int d^3 x f(\boldsymbol{x}' - \boldsymbol{x}) \dot \phi(x)
\end{aligned}
\end{split}\]
其中
(248) \[\begin{equation}
f(\boldsymbol{x}' - \boldsymbol{x}) = \int \frac{d^3 k}{(2\pi)^{3} 2 \omega_k} e^{i \boldsymbol{k} \cdot (\boldsymbol{x}' - \boldsymbol{x})}
\end{equation}\]
我们看到,尽管\(\phi(x)\) 是定域的,但\(\phi^-(x)\) 并非如此。(247) 中的\(f(\boldsymbol{x}' - \boldsymbol{x})\) 导致了非定域性。即然\(\phi^\pm\) 是定域的,它们的关联函数存在因果律破坏就不足为奇了。
测量和对易子
解决上述问题的关键在于重新审视因果律的定义。问题出在\(\Delta_+(x-y)\) 并非物理可测量量。原因是,\(\Delta_+(x - y)\) 想计算的是从\(y\) 点产生一个粒子传播到\(x\) 的概率幅,这个问题隐含了\(y\) 发生在\(x\) 之前这一假设。担当\(x\) 和\(y\) 处于类空间隔时,存在洛伦兹变换使得\(x\) 和\(y\) 的时间顺序被反转,这时从\(y\) 点产生一个粒子传播到\(x\) 的概率幅这一问题变得没有意义。
正确的做法是,我们在\(x\) 和\(y\) 分别做一次任意的测量。我们问,这两次测量是否可交换顺序而不改变测量结果?如是的话,则两个事件间不存在因果联系。在量子力学中,测量可以表示成一个算符\(O\) 。在量子场论里,这个算符应该是场算符的函数。因此,测量可对易的要求可以写为
(249) \[\begin{equation}
[O_1(\phi), O_2(\phi)] = 0
\end{equation}\]
或者更简单的,
(250) \[\begin{equation}
[\phi(x), \phi(y)] = 0
\end{equation}\]
这个条件称为局域性条件 。将\(\phi = \phi^+ + \phi^-\) 代入,我们得到
(251) \[\begin{align}
[\phi^+(x) + \phi^-(x), \phi^+(y) + \phi^-(y)] =&\ [\phi^+(x), \phi^-(y)] + [\phi^-(x), \phi^+(y)]
\\
=&\ - \Delta_+ (y-x) + \Delta_+ (x-y)
\end{align}\]
令\(V^\mu = x^\mu - y^\mu\) ,则上式无非是
(252) \[\begin{equation}
[\phi(x), \phi(y)] = \Delta_+ (V) - \Delta_+ (-V)
\end{equation}\]
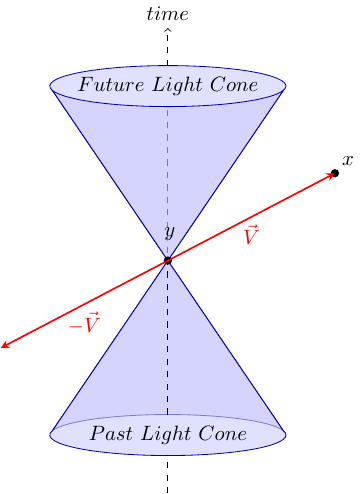
对于类空间隔\(V^2 < 0\) ,在时空图上可以表示为
容易找到一个连续 洛伦兹变换将\(V\) 变为\(-V\) ,
(253) \[\begin{equation}
V^\mu \to \Lambda^\mu_{\ \nu} V^\nu = - V^\mu
\end{equation}\]
因此,由(245) ,我们有
(254) \[\begin{equation}
[\phi(x), \phi(y)] = \Delta_+ (V) - \Delta_+ (-V) = \Delta_+ (V) - \Delta_+ (\Lambda V) = 0
\end{equation}\]
关于\([\phi(x), \phi(y)]\) 在类空间隔上为零的物理解释,我们在学完复标量场后再讨论。
与克莱因-戈登方程格林函数的关系
下来我们来看前面定义的Wightman函数和克莱因-戈登方程的联系。将克莱因-戈登方程作用到Wightman函数上:
(255) \[\begin{align}
(\partial_x^2 + m^2) \Delta_+(x - y) &= \langle 0 | (\partial_x^2 + m^2) \phi(x) \phi(y) |0\rangle \\
&= 0
\end{align}\]
其中我们应用了
(256) \[\begin{equation}
(\partial_x^2 + m^2) \phi(x) = 0
\end{equation}\]
因此,Wightman函数是克莱因-戈登方程的解。
在以后关于相互作用的讨论中,我们还将碰所谓的两点编时函数,也称作费曼传播子,记作:
(257) \[
\begin{equation}
G_F(x - y) = \langle 0 | T [\phi(x) \phi(y) ] |0\rangle
\end{equation}
\]
其中编时算符\(T\) 的作用为
(258) \[\begin{equation}
T[ \phi(x) \phi(y) ] = \theta(x^0 - y^0) \phi(x) \phi(y) + \theta(y^0 - x^0) \phi(y) \phi(x)
\end{equation}\]
其中阶跃函数的定义为
(259) \[\begin{equation}
\theta(x) = \begin{cases}
1 & x > 0 \\
0 & x < 0
\end{cases}
\end{equation}\]
将克莱因-戈登算符作用到费曼传播子上,我们有
(260) \[\begin{align}
(\partial_x^2 + m^2) G_F(x - y) &= \langle 0 | (\partial_x^2 + m^2) T [\phi(x) \phi(y) ] |0\rangle \\
\\
&= \langle 0 | (\partial_x^2 + m^2)
\Big[\theta(x^0 - y^0) \phi(x) \phi(y) + \theta(y^0 - x^0) \phi(y) \phi(x) \Big] |0\rangle \\
\end{align}\]
显然,当克莱因-戈登算符作用到\(\phi(x)\) 上时立刻给出零。我们得到
(261) \[\begin{align}
(\partial_x^2 + m^2) G_F(x - y) &= \langle 0 | \delta'(x^0 - y^0) \phi(x) \phi(y) + \delta'(y^0 - x^0) \phi(x) \phi(y) |0\rangle \\
&\ + 2 \langle 0 | \delta(x^0 - y^0) \dot \phi(x) \phi(y) - \delta(y^0 - x^0) \phi(y) \dot \phi(x) |0\rangle
\end{align}\]
其中我们应用了
(262) \[\begin{equation}
\theta'(x) = \delta(x)
\end{equation}\]
注意到\(\delta\) 函数及其导数应在分布的意义上理解。物理场应满足在无穷远边界衰减的条件,因此可以对上式中delta函数的微分项作分部积分操作,得到
(263) \[\begin{align}
(\partial_x^2 + m^2) G_F(x - y) = &\ - \langle 0 | \delta(x^0 - y^0) \dot \phi(x) \phi(y) |0 \rangle + \langle 0 | \delta(y^0 - x^0) \phi(y) \dot \phi(x) |0\rangle
\\
&\ + 2 \langle 0 | \delta(x^0 - y^0) \dot \phi(x) \phi(y) |0 \rangle - 2 \langle 0|\delta(y^0 - x^0) \phi(y) \dot \phi(x) |0\rangle
\end{align}\]
即
(264) \[\begin{equation}
(\partial_x^2 + m^2) G_F(x - y) = \delta(x^0 - y^0) \langle 0 | [\pi(x), \phi(y)] |0\rangle
\end{equation}\]
利用场的等时正则对易关系,
(265) \[\begin{equation}
[\pi(x), \phi(y)] = -i \delta^{(3)}(\boldsymbol{x} - \boldsymbol{y})
\end{equation}\]
我们得到
(266) \[\begin{equation}
(\partial_x^2 + m^2) G_F(x - y) = - i \delta(x^0 - y^0) \delta^{(3)}(\boldsymbol{x} - \boldsymbol{y}) = -i \delta^{(4)}(x-y)
\end{equation}\]
这表明,费曼传播子是克莱因-戈登方程的格林函数。
注意到,克莱因-戈登方程是二阶微分方程,因此如果想从这个微分方程唯一确定费曼传播子的话,我们还需要指定边界条件。我们从动量空间出发来确定边界条件。费曼传播子的傅里叶变换为
(267) \[\begin{equation}
G_F(x) = \int \frac{d^4 x}{(2 \pi)^4} e^{-ikx} G_F(k)
\end{equation}\]
简单起见我们仅通过宗量的不同来区分坐标空间和动量空间函数。将上式代入克莱因-戈登方程,我们有
(268) \[\begin{equation}
(-k^2 + m^2) G_F(k) = -i
\end{equation}\]
这个方程的解为
(269) \[\begin{equation}
G_F(k) = \frac{i}{k^2 - m^2 + i \epsilon}
\end{equation}\]
其中\(\epsilon\) 是一个无穷小正数,它的引入唯一指定了边界条件,此时的坐标空间费曼传播子写为
(270) \[
\begin{equation}
G_F(x) = \int \frac{d^4 k}{(2 \pi)^4} \frac{i e^{-ikx}}{k^2 - m^2 + i \epsilon}
\end{equation}
\]
让我们来证明这确实给出(257) 中的费曼传播子。我们先考虑动量积分的能量分量:
(271) \[\begin{align}
G_F(x) = \int_{-\infty}^\infty dk^0 \int \frac{d^3 k}{(2 \pi)^4 } \frac{i e^{-i \boldsymbol{k} \cdot \boldsymbol{x}}}{(k^0 - \omega_k + i \epsilon)(k^0 + \omega_k - i \epsilon)}
\end{align}\]
其中\(\omega_k = \sqrt{\boldsymbol{k}^2 + m^2}\) 。上式中我们应用了在\(\epsilon \to 0_+\) 时成立的等式
(272) \[\begin{equation}
\frac{1}{k^2 - m^2 + i \epsilon} = \left( \frac{1}{k^0 - \omega_k + i \epsilon} \cdot \frac{1}{k^0 + \omega_k - i \epsilon} \right)
\end{equation}\]
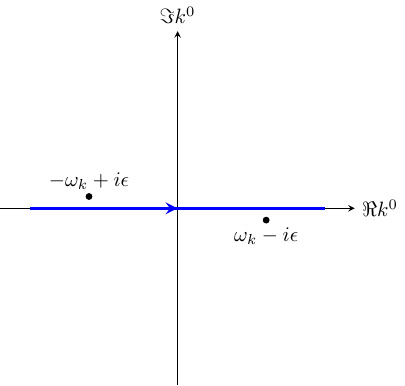
当\(x^0 > 0\) 时,\(e^{-i k^0 x^0}\) 因子在下半平面收敛,因此可以选取下半圆弧构成封闭围道。仅有
\[
\frac{1}{k^0 - \omega_k + i \epsilon}
\]
在围道内。利用柯西定理(注意我们选取的围道是顺时针围道,因此柯西定理存在一个额外负号),我们得到
(273) \[\begin{equation}
G_F(x) \Big|_{x^0 > 0} = \int \frac{d^3 k}{(2 \pi)^3 } \frac{e^{ -i \omega_k x^0 + i \boldsymbol{k} \cdot \boldsymbol{x}}}{2 \omega_k} = \Delta_+(x)
\end{equation}\]
同理,当\(x^0 < 0\) 时,\(e^{-i k^0 x^0}\) 因子在上半平面收敛,这时积分结果为
(274) \[\begin{equation}
G_F(x) \Big|_{x^0 < 0} = \int \frac{d^3 k}{(2 \pi)^3 } \frac{e^{ i \omega_k x^0 - i \boldsymbol{k} \cdot \boldsymbol{x}}}{2 \omega_k} = \Delta_+(-x)
\end{equation}\]
综合上述两式即得到
(275) \[\begin{equation}
G_F(x) = \Delta_+(x) \theta(x^0) + \Delta_+(-x) \theta(-x^0)
\end{equation}\]
上述计算中的费曼传播子所对应的围道如下图所示:
注意费曼传播子在类空间隔上并不为零。例如,让\(x^0=y^0\) ,则
(276) \[\begin{equation}
G_F(x - y) = \langle 0 | \phi(x) \phi(y) | 0 \rangle = \Delta_+(x - y) \neq 0
\end{equation}\]
此外,从费曼传播子的动量空间表示(270) 可以看出它是显式洛伦兹不变的。
费曼传播子的物理意义我们留待以后再讲。
在经典电动力学中,我们还学过另外两类传播子:推迟(retarded)和超前(advanced)传播子。推迟传播子的定义为
(277) \[\begin{equation}
\Delta_R(x-y) = \theta(x^0 - y^0) \langle 0 | [\phi(x), \phi(y)] | 0 \rangle
\end{equation}\]
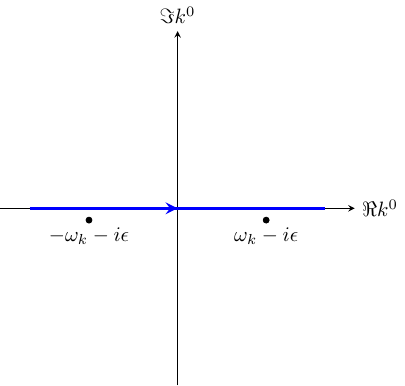
从这个定义中可以看出,推迟传播子不是洛伦兹协变的,但在光锥之外为零。推迟传播子的定义也隐含了它的边界条件。不妨令\(y=0\) ,则\(G_R(x)\) 在\(x^0 < 0\) 时为零。为了满足这个边界条件,注意到\(e^{-i k^0 x^- }\) 在\(x^0 < 0\) 时在上半平面收敛,因此可以选取上半圆弧构成封闭围道并要求极点在围道外部,即
(278) \[\begin{equation}
G_R(x) = \int \frac{d^4 k}{(2 \pi)^4} \frac{i e^{-ikx}}{(k^0 + i \epsilon)^2 - \boldsymbol{k}^2 - m^2}
\end{equation}\]
对应的极点位形如下图所示:
当\(x^0>0\) 时,围道应向下半平面绕,此时两个极点均落入围道中。这时的积分结果为:
(279) \[\begin{align}
G_R(x) =&\ 2\pi \int \frac{d^3 k}{(2 \pi)^3} \left[ \frac{1}{2 \omega_k} e^{- i (\omega_k - i\epsilon) x^0 + i \boldsymbol{k} \cdot \boldsymbol{x}} - \frac{1}{2 \omega_k} e^{-i (-\omega_k - i \epsilon) x^0 + i \boldsymbol{k} \cdot \boldsymbol{x}} \right]
\\
=&\ \langle 0 | \phi(x) \phi(0) | 0 \rangle - \langle 0 | \phi(0) \phi(x) | 0 \rangle
\\
= &\ \langle 0 | [\phi(x), \phi(0)] | 0 \rangle
\end{align}\]
其中应用了\(\boldsymbol{k} \to - \boldsymbol{k}\) 的对称性:
(280) \[\begin{equation}
\int \frac{d^3 k}{(2 \pi)^3 2 \omega_k} e^{i \omega_k x^0 + i \boldsymbol{k} \cdot \boldsymbol{x}} = \int \frac{d^3 k}{(2 \pi)^3 2 \omega_k} e^{i \omega_k x^0 - i \boldsymbol{k} \cdot \boldsymbol{x}} = \langle 0 | \phi(0) \phi(x) | 0 \rangle
\end{equation}\]
类似的,超前传播子可以定义为
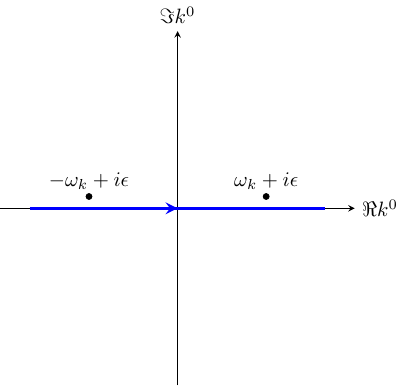
(281) \[\begin{equation}
\Delta_A(x-y) = - \theta(y^0 - x^0) \langle 0 | [\phi(x), \phi(y)] | 0 \rangle
\end{equation}\]
相应的动量空间极点形变为下图所示