QED单圈修正的计算

Lagrangian

The renormalized QED Lagrangian we use is as follows:

\[ {\cal L} = - \frac{1}{4} Z_3 F_{\mu\nu} F^{\mu\nu} + Z_2 \bar{\psi} (i \gamma^\mu \partial_\mu - Z_m m) \psi - Z_1 e \mu^\epsilon \bar{\psi} \gamma^\mu A_\mu \psi \]

The renormalized perturbation theory is achieved by splitting the lagrangian above appropriately:

(935)\[\begin{align} {\cal L} =&\ - \frac{1}{4} F_{\mu\nu} F^{\mu\nu} + \bar{\psi} (i \gamma^\mu \partial_\mu - m) \psi - i e \mu^\epsilon \bar{\psi} \gamma^\mu A_\mu \psi \\ &\ - \frac{1}{4}(Z_3 - 1) F_{\mu\nu} F^{\mu\nu} + (Z_2 - 1) \bar{\psi} i \gamma^\mu \partial_\mu \psi - (Z_2 Z_m - 1) m \bar \psi \psi - i (Z_1 - 1) e \mu^\epsilon\bar{\psi} \gamma^\mu A_\mu \psi \end{align}\]

Calculation of photon self-energy diagram

(*Import Feyncalc*)
<< FeynCalc`

FeynCalc 9.3.1 (stable version). For help, use the documentation center,\
 
>    check out the wiki or visit the forum.

To save your and our time, please check our FAQ
 
>    for answers to some common FeynCalc questions.

See also the supplied examples. If you use FeynCalc in your research, please\
 
>    cite

 \[Bullet] V. Shtabovenko, R. Mertig and F. Orellana, Comput.Phys.Commun. 256\
 
>   (2020) 107478, arXiv:2001.04407.

 \[Bullet] V. Shtabovenko, R. Mertig and F. Orellana, Comput.Phys.Commun. 207\
 
>   (2016) 432-444, arXiv:1601.01167.

 \[Bullet] R. Mertig, M. Bo"hm, and A. Denner, Comput. Phys. Commun. 64\
 
>   (1991) 345-359.

Define the One-Particle-Irreducible (1PI) diagram of the photon self energy as \(i \Pi_{\mu\nu} (q)\). Ward identidy implies:

\[ q^\mu \Pi_{\mu\nu}(q) = 0 \]

Which imples that \(\Pi_{\mu\nu}\) can be uniquely decomposed as

\[ \Pi_{\mu\nu}(q) = (\eta_{\mu\nu} q^2 - q_\mu q_\nu) \Pi(q^2) \]

We shall check this decomposition from explicit calculation. At one-loop, the Feynman diagram for \(i \Pi_{\mu\nu}(q^2)\) is given by:

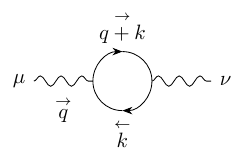
From the Feynman rule, we can read off the one-loop diagram as:

(936)\[\begin{equation} i \Pi^{\mu\nu}(q) = - (-i e)^2 i^2 \mu^{2\epsilon}\int \frac{d^d k}{(2 \pi)^d} \frac{\mathrm{Tr} \Big[ ( \gamma^\rho k_\rho + m) \gamma^\nu (\gamma^\sigma (q+k)_\sigma + m) \gamma^\mu\Big] }{((q+k)^2 - m^2 + i \epsilon) (k^2 - m^2 + i \epsilon) } \end{equation}\]

Let’s evaulate the trace first. define

(937)\[\begin{equation} Num =- (-i e)^2 i^2 \mathrm{Tr} \Big[ ( \gamma^\rho k_\rho + m) \gamma^\nu (\gamma^\sigma (q+k)_\sigma + m) \gamma^\mu\Big] \end{equation}\]

We can easily evaulate it in Mathematica with the help of FeynCalc:

num1=-(-I e)^2*I^2*Tr[(GSD[k]+m).GAD[\[Nu]].(GSD[q+k]+m).GAD[\[Mu]]]

We can combine the numerator using Feynman’s parameterization:

(938)\[\begin{align} \frac{1}{((q+k)^2 - m^2 + i \epsilon) (k^2 - m^2 + i \epsilon) } =&\ \int_0^1 dx\, \frac{1}{x ((q+k)^2 - m^2)+ (1-x) (k^2 - m^2)} \\ =&\ \int_0^1 dx\, \frac{1}{k^2 + 2 x k \cdot q + x q^2 - m^2} \\ =&\ \int_0^1 dx\, \frac{1}{(k + x q)^2 - m^2 + x (1-x) q^2} \\ = &\ \int_0^1 dx\, \frac{1}{[(k + x q)^2 - \Delta]^2}\,, \qquad \Delta = m^2 - x(1-x) q^2 - i \epsilon \end{align}\]

This suggest that we should shift the loop momentum as \(l^\mu = k^\mu + x q^\mu\). Applying this momentum shift to the numerator, we get:

(*make a momentum shift k->l - x q*)
FCE[num1]//InputForm
num2=FCE[num1]/.{FVD[k,a_]:>FVD[l,a]-x*FVD[q,a], SPD[k,k]:>SPD[l,l]-2*x*SPD[l,q]+x^2*SPD[q,q], SPD[k,q]:>SPD[l,q]-x*SPD[q,q]}//Expand

Now we can drop all terms linear in \(l\), and replace \(l^\mu l^\nu\) by \(l^2 \eta^{\mu\nu}/d\):

num3=FCE[num2]/.{FVD[l,\[Mu]] FVD[l,\[Nu]]->SPD[l,l]*MTD[\[Mu],\[Nu]]/d}/.{SPD[l,q]:>0}/.{FVD[l,_]:>0}//Collect[#,SPD[l,l],Simplify]&

We now have two different integrals to evaluate:

(939)\[\begin{align} I_1 = &\ \frac{4 (d-2) e^2 g^{\mu \nu }}{d} \mu^{2\epsilon} \int_0^1 dx \int \frac{d^d l}{(2 \pi)^d} \frac{l^2}{(l^2 - \Delta)^2} \\ I_2 = &\ -4 e^2 \left(g^{\mu \nu } \left(m^2-q^{} (x-1) x\right)+2 (x-1) x q^{\mu } q^{\nu }\right) \mu^{2\epsilon}\int_0^1 dx \int \frac{d^d l}{(2 \pi)^d} \frac{1}{(l^2 - \Delta)^2} \end{align}\]

Substituting the known integrals in \(d\) dimensions:

(940)\[\begin{align} \int \frac{d^d l}{(2 \pi)^d} \frac{1}{(l^2 - \Delta)^n} =&\ \frac{i (-1)^n}{(4 \pi)^{d/2}} \frac{\Gamma(n - d/2)}{\Gamma(n)} \Delta^{d/2 - n} \\ \int \frac{d^d l}{(2 \pi)^d} \frac{l^2}{(l^2 - \Delta)^n} =&\ \frac{i (-1)^{n-1}}{(4 \pi)^{d/2}} \frac{\Gamma(n - d/2 -1 )}{\Gamma(n)} \Delta^{d/2 +1 - n} \frac{d}{2} \end{align}\]

int1[d_,n_,delta_]:=I*(-1)^n/(4*Pi)^(d/2)*Gamma[n-d/2]/Gamma[n]*delta^(d/2-n);
int2[d_,n_,delta_]:=I*(-1)^(n-1)/(4*Pi)^(d/2)*Gamma[n-d/2-1]/Gamma[n]*delta^(d/2+1-n)*d/2;

Expanding to \({\cal O}(\epsilon)\), the sum of the \(I_1\) and \(I_2\) is now given by (Note that at this step we have adopt the \(\overline{\mathrm{MS}}\) scheme, where the renormalization scale is modified to be \(\mu^2 \to \mu^2 (4 \pi)^{-\epsilon} e^{\epsilon \gamma_E}\)):

sum1=Coefficient[num3,SPD[l,l]]*int2[d,2,Δ]+(num3/.SPD[l,l]->0)*int1[d,2,Δ];
sum2=Series[(4*Pi)^(-eps)*Exp[eps*EulerGamma]*\[Mu]^(2*eps)*sum1/.{d->4-2*eps},{eps,0,0}]//Normal

(*Substitute in the value of Delta*)
myDelta=m^2-x*(1-x)*SPD[q,q];
sum3=sum2/.Δ->myDelta//Simplify//Collect[#,eps]&

(*Perform the x integral*)
sum4=Integrate[sum3,{x,0,1},GenerateConditions->False]

sum5=Collect[sum4/.SPD[q,q]->q^2,eps]//Simplify[#,Assumptions->{q>0}]&//Collect[#,eps]&

(*Let m^2=r*q^2*)
sum6=sum5//Simplify[#,Assumptions->{q>0}]&//Collect[#,eps]&

(*and for q^2->0, this result for Pi(q^2=0) becomes*)
sum7=Coefficient[Series[Coefficient[(-I)*sum6,MTD[\[Mu],\[Nu]]],{q,0,2}]//Normal//Simplify[#,Assumptions->{q>0}]&//Collect[#,eps]&,q^2]/.e^2->alpha*(4*Pi)

Now Let’s consider the Dyson series for the photon self-energy diagram:

(941)\[\begin{align} & \frac{-i \eta_{\mu\nu}}{q^2+i \epsilon} + \frac{-i \eta_{\mu\rho}}{q^2+i \epsilon} (i (q^2 \eta_{\rho\sigma} - q_\rho q_\sigma) \Pi(q^2)) \frac{-i \eta_{\sigma\nu}}{q^2+i \epsilon} + \cdots \\ =& \frac{-i \eta_{\mu\nu}}{q^2 (1 - \Pi(q^2))} + \text{terms proportional to } q_\mu q_\nu \end{align}\]

The terms proportional to \(q_\mu q_\nu\) vanishes when contracted with a fermion line by Ward identity, therefore can be neglected. We now find that the exact Kallen-Lehmann propagator for photon is given by

(942)\[\begin{equation} \Delta_{\mu\nu}(q) = \frac{-i \eta_{\mu\nu}}{q^2 (1 - \Pi(0))} + \cdots \end{equation}\]

where the \(\cdots\) represents the continous spectrum of the photon. We see that the mass of photon is not renormalized in perturbation theory, as it shouldn’t. The renormalization constant \(Z_3\) is therefore given by

(943)\[\begin{equation} Z_3 = (1 - \Pi(0))^{-1} \end{equation}\]

Substitute the explicit one-loop result we obtained previously, we found

(944)\[\begin{equation} Z_3 = 1 + \frac{\alpha_s}{3\pi} \left[ - \frac{1}{ \epsilon} + \ln \frac{m^2}{\mu^2} \right] \end{equation}\]