初见量子场论

量子简谐振子

The career of a young theoretical physicist consists of treating the harmonic oscillator in ever-increasing levels of abstraction.

—Sidney Coleman

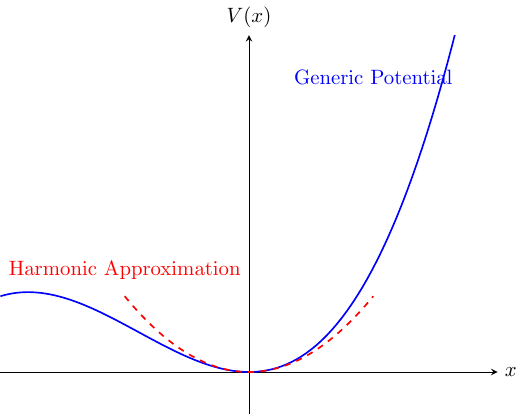
简谐振子振子是大家再熟悉不过的概念。尽管简单， 但它是本课程的基础。考虑一个一维势场\(V(x)\)中粒子在平衡位置\(x_0\)附近的小振动，可以将势能在平衡位置附近展开：

(48)\[\begin{equation} V(x) = V(x_0) + (x - x_0) \frac{dV}{dx} \Bigg|_{x_0} + \frac{1}{2} (x - x_0)^2 \frac{d^2V}{dx^2} \Bigg|_{x_0} + \cdots \end{equation}\]

其中第一项是势能零点，我们总可以方便地取为零，而第二项\(dV/dx\)在平衡位置处为零，因此也可以略去。忽略掉三阶及更高阶的项，我们发现平衡位置附近的运动总可以近似为一个简谐振动。因此，理解简谐振子是理解任何平衡位置附近振动系统的基础。

在标准量子力学课程中，求解简谐振子的能级和波函数可以归结为求解如下不含时薛定谔方程：

(49)\[ \begin{equation} \hat{H} \Psi(x) = E \Psi(x) \end{equation} \]

其中

(50)\[\begin{equation} \hat{H} = \frac{1}{2m} \hat{p}^2 + \frac{1}{2} m \omega^2 \hat{x}^2 \end{equation}\]

是简谐振子系统的哈密顿量算符， 其中\(\hat{p}\)和\(\hat{x}\)分别是动量算符和位置算符。 在经典力学中，正则坐标和正则动量满足泊松括号关系：

(51)\[\begin{equation} \{x, p\}_{\rm PB} := \frac{\partial x}{\partial x} \frac{\partial p}{\partial p} - \frac{\partial x}{\partial p} \frac{\partial p}{\partial x} = 1 \end{equation}\]

正则量子化方案下泊松括号变成坐标和动量算符的对易子：

(52)\[\begin{equation} \lim_{ \hbar \to 0} \frac{1}{i \hbar} [\hat{x}, \hat{p}] = \{x, p\}_{\rm PB} = 1 \end{equation}\]

在坐标表象下，

(53)\[\begin{equation} \hat{x} \Psi(x) = x \Psi(x) \,, \qquad \hat{p} \Psi(x) = -i \hbar \frac{d}{dx} \Psi(x) \end{equation}\]

因此(49)是关于波函数\(\Psi(x)\)的二阶微分方程，求解这个二阶微分方程，我们可以得到简谐振子的能级和波函数。

求解简谐振子的另一种方法是使用产生湮灭算符，也叫做阶梯算符。我们将看到，这种方法能够直接推广到量子场论。其核心思想是将简谐振子的哈密顿量因子化。 为此，我们作如下的变换：

(54)\[\begin{equation} a = \sqrt{\frac{m \omega}{2}} \hat{x} + \frac{i}{\sqrt{2 m \omega}} \hat{p} \,, \qquad a^\dagger = \sqrt{\frac{m \omega}{2}} \hat{x} - \frac{i}{\sqrt{2 m \omega}} \hat{p} \end{equation}\]

容易验算

(55)\[\begin{align} a^\dagger a = &\ \left(\sqrt{\frac{m \omega}{2}} \hat{x} - \frac{i}{\sqrt{2 m \omega}} \hat{p}\right) \left( \sqrt{\frac{m \omega}{2}} \hat{x} + \frac{i}{\sqrt{2 m \omega}} \hat{p}\right) \\ =&\ \frac{m \omega}{2} \hat{x}^2 + \frac{1}{2 m \omega} \hat{p}^2 + \frac{i}{2} [\hat{x}, \hat{p}] \end{align}\]

因此简谐振子的哈密顿量可以写为

(56)\[\begin{equation} \hat{H} = \omega \left( a^\dagger a + \frac{\hbar}{2} \right) \end{equation}\]

这里\(a\)和\(a^\dagger\)分别是湮灭算符和产生算符，满足

(57)\[\begin{equation} [a, a^\dagger] := a a^\dagger - a^\dagger a =\hbar\,, \quad [a, a] = [a^\dagger, a^\dagger] = 0 \end{equation}\]

他们与哈密顿量的对易关系为

(58)\[\begin{equation} [\hat{H}, a] = - \omega \hbar a \,, \qquad [\hat{H}, a^\dagger] = \omega \hbar a^\dagger \end{equation}\]

设\(|E\rangle\)是哈密顿量的能量本征态，

(59)\[\begin{equation} \hat{H} |E\rangle = E |E\rangle \end{equation}\]

则在产生湮灭算符作用后仍然是能量本征态：

(60)\[\begin{equation} \hat{H} a^\dagger |E\rangle = (E + \omega \hbar) a^\dagger |E\rangle \,, \qquad \hat{H} a |E\rangle = (E - \omega \hbar) a |E\rangle \end{equation}\]

但相应的能量增加或减少\(\omega \hbar\)。一个稳定的量子系统要求存在最低能态。因此，必然存在某个态\(|0\rangle\)，使得

(61)\[\begin{equation} a |0\rangle = 0 \end{equation}\]

这个态称作基态。一个非常重要的事实是简谐振子基态也具有非零能量

(62)\[\begin{equation} \hat{H} |0\rangle = \frac{\omega \hbar}{2} |0\rangle \end{equation}\]

称作零点能。我们在后面还会反复遇到它。

我们可以通过产生算符作用在基态上得到一系列态

(63)\[\begin{equation} |n\rangle = \frac{(a^\dagger)^n}{\sqrt{n!}} |0\rangle \end{equation}\]

其中因子\(1/\sqrt{n!}\)是为了归一化，\(n\)称作占有数。容易得到，不同占有数的态是正交的：

(64)\[\begin{equation} \langle m | n \rangle = \delta^{mn} \end{equation}\]

这些态称作Fock态。 容易验证\(\hat{N} := a^\dagger a/\hbar\)是简谐振子的占有数算符，满足

(65)\[\begin{equation} [\hat{N}, a] = - a \,, \qquad [\hat{N}, a^\dagger] = a^\dagger \end{equation}\]

当作用在态\(|n \rangle\)上时给出

(66)\[\begin{equation} \hat{N} |n\rangle = n |n\rangle \end{equation}\]

哈密顿量用占有数算符可以写为，

(67)\[\begin{equation} \hat{H} = \omega \hbar \left( \hat{N} + \frac{1}{2} \right) \end{equation}\]

作用在态\(|n\rangle\)上的本征值为

(68)\[\begin{equation} \hat{H} |n\rangle = \omega \hbar \left( n + \frac{1}{2} \right) |n\rangle \end{equation}\]

作业

验证本节中出现的所有对易关系。鼓励同学们写一段mathematica程序自动计算这些对易关系。

我们进一步讨论一下量子谐振子的性质。下面这一段Mathematica代码画出了经典谐振子势能曲线，量子谐振子能级，以及量子谐振子波函数模方\(|\Psi_n(x)|^2\)。

(*Set parameters*)m = 1;
\[Omega] = 1;
\[HBar] = 1;
\[Beta] = Sqrt[m \[Omega]/\[HBar]];
(*Define potential energy function*)
V[x_] := 1/2 m \[Omega]^2 x^2;

(*Define energy levels*)
En[n_] := \[HBar] \[Omega] (n + 1/2);

(*Define Hermite polynomials*)
H[n_, x_] := HermiteH[n, x];

(*Define wave functions*)
\[Psi][n_, x_] := (Sqrt[\[Beta]]/Sqrt[2^n n! Sqrt[\[Pi]]])*
   Exp[-(\[Beta] x)^2/2]*H[n, \[Beta] x];

(*Plot potential energy curve and energy levels*)
potentialPlot = 
  Plot[V[x], {x, -4, 4}, PlotStyle -> {Thick, Blue}, 
   PlotRange -> {0, 6}, Frame -> True, FrameLabel -> {"x", "Energy"}, 
   PlotLabel -> 
    "Harmonic Oscillator: Classical Potential and Quantum Energy \
Levels"];

energyLevels = Table[Line[{{-4, En[n]}, {4, En[n]}}], {n, 0, 5}];

Show[potentialPlot, Graphics[{Red, energyLevels}], 
 PlotRange -> {{-4, 4}, {0, 6}}]

(*Plot wave functions squared*)
waveFunctionPlot = 
 Plot[Evaluate[Table[\[Psi][n, x]^2 + En[n], {n, 0, 5}]], {x, -4, 4}, 
  PlotRange -> {0, 6}, 
  PlotStyle -> {Red, Green, Blue, Orange, Purple, Brown}, 
  Frame -> True, FrameLabel -> {"x", "Energy"}, 
  PlotLabel -> "Harmonic Oscillator: Wave Functions Squared", 
  PlotLegends -> 
   Placed[LineLegend[{"n = 0", "n = 1", "n = 2", "n = 3", "n = 4", 
      "n = 5"}, LegendFunction -> "Panel"], {0.85, 0.65}]]

(*Combine plots*)
Show[potentialPlot, waveFunctionPlot, Graphics[{Red, energyLevels}], 
 PlotRange -> {{-4, 4}, {0, 6}}]

结果如图所示：

通常，实验测量的是两个能级之差，这时零点能不具有可观测效应。为了简单起见，可以将零点能设为零。这可以通过定义如下正规排序(Normal Order)实现：

Important

正规排序 对于由玻色子产生湮灭算符的乘积所构成的算符，我们定义正规排序为将产生算符放在左边，湮灭算符放在右边，用记号\(:\cdots:\)表示。

例如:

(69)\[\begin{align} :a a^\dagger: =&\ a a^\dagger \\ :a^\dagger a: =&\ a^\dagger a \\ :a a a^\dagger: =&\ a^\dagger a a \\ :a^\dagger a a a^\dagger a a a^\dagger: =&\ (a^\dagger)^3 a^4 \end{align}\]

注意，不能在正规排序内部应用对易关系，否则会得到矛盾结果。例如，对于 \(a a^\dagger\)，按照上式有\(:a a^\dagger: = a^\dagger a\)，但如果在正规排序内部应用对易关系则得到\(:a a^\dagger: = :a^\dagger a + \hbar:\)，这显然是错误的。

作业

证明：对于谐振子粒子数算符\(\hat{N} = a^\dagger a/\hbar\)，有

(70)\[\begin{equation} :\hat{N}^k: = \hat{N} (\hat{N} - 1) \cdots (\hat{N} - k + 1) \end{equation}\]

耦合谐振子链的量子化

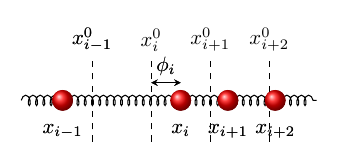
上一节的方法可以直接推广到多个谐振子的情形。考虑含\(N\)个原子的一维原子链，原子间距为\(a\)，原子质量为\(m\)。第\(i\)个原子的坐标记为\(x_i\)，相对其平衡位置处的位移记为\(\phi_i = x_i - x_i^0\)，其中\(x_i^0\)是平衡位置，如下图所示。

原子链长\(L = Na\)。对于充分大的\(N\)，边界条件对内部原子的运动影响不大，因此简化起见，我们考虑周期性边界条件，即\(\phi_{N+n} = \phi_n\)。

假设原子间只存在近邻相互作用，相互作用势能为\(V(\phi_n - \phi_{n+1})\)。对于平衡位置附近的微小振动，我们可以将势能展开到二阶谐振子势：

(71)\[\begin{equation} V(\phi_n - \phi_{n+1}) = \frac{1}{2} K (\phi_n - \phi_{n+1})^2 + {\cal O}( (\phi_n - \phi_{n+1})^3 ) \end{equation}\]

其中\(K\)是弹性常数。这样，原子链的经典哈密顿量可以写为

(72)\[\begin{equation} H = \sum_{n=1}^N \left[ \frac{\pi_n^2}{2m} + \frac{K}{2} (\phi_{n+1} - \phi_n)^2 \right] \end{equation}\]

其中\(\pi_n = m \dot \phi_n\)是第\(n\)个原子的动量。一般来说，\(\phi_n\)和\(\pi_n\)是时间的函数，但由于能量是守恒量，我们这里不显式标出时间依赖。

如何量子化这个系统是直接的。让我们讨论\(t=0\)时刻的量子化。我们将位移\(\phi_n(0)\)和动量\(\pi_n(0)\)提升为算符，并要求其满足对易关系：

(73)\[\begin{equation} [\phi_n, \pi_m] = i \hbar \delta_{nm} \end{equation}\]

但这个量子系统的哈密顿量并非简单的\(N\)个简谐振子哈密顿量之和，其差异来自于紧邻耦合项\(\phi_n \phi_{n+1}\)。

基于我们边界条件选取，可以注意到哈密顿量具有如下的分立平移对称性：

(74)\[\begin{equation} \phi_n \to \phi_{n+1} \,, \qquad \pi_n \to \pi_{n+1} \end{equation}\]

这启发我们变换到动量空间使得平移对称性更加明显。我们定义分立傅立叶变换

(75)\[\begin{align} \phi_n =&\ \frac{1}{\sqrt{N}} \sum_{q} e^{i q n a} \phi_q \\ \pi_n =&\ \frac{1}{\sqrt{N}} \sum_{q} e^{i q n a} \pi_q \end{align}\]

对应的逆变换为

(76)\[\begin{align} \phi_q =&\ \frac{1}{\sqrt{N}} \sum_{n} e^{-i q n a} \phi_n \\ \pi_q =&\ \frac{1}{\sqrt{N}} \sum_{n} e^{-i q n a} \pi_n \end{align}\]

周期边界条件要求

(77)\[\begin{equation} \phi_{n+N} = \frac{1}{\sqrt{N}} \sum_{q} e^{i q (n+N) a} \phi_q = \phi_n \end{equation}\]

即

(78)\[\begin{equation} e^{i q N a} = 1 \end{equation}\]

因此动量的取值也是分立的

(79)\[\begin{equation} q N a = 2 \pi m \,, \quad m \in \mathbb{Z} \end{equation}\]

或者

(80)\[\begin{equation} q = \frac{2 \pi m}{L} \end{equation}\]

实空间的周期性同时意味着动量空间的周期性， 由于

(81)\[\begin{equation} e^{ i (q+\frac{2 \pi}{a}) n a} = e^{i q n a} \end{equation}\]

因此\(q\)的周期为\(2 \pi/a\)。我们可以将\(q\)取值范围限制在\(0 \le q < 2 \pi/a\)。 可以验证

(82)\[\begin{equation} \phi_n = \frac{1}{\sqrt{N}} \sum_{q} e^{i q n a} \phi_q = \frac{1}{\sqrt{N}} \sum_{q} e^{i q n a} \frac{1}{\sqrt{N}} \sum_{n'} e^{-i q n' a} \phi_{n'} = \phi_n \end{equation}\]

其中我们应用了

(83)\[\begin{equation} \sum_{q} e^{i q (n - n') a} = \sum_{m=0}^{N-1} e^{i 2 \pi (n - n') m/N} = N \delta_{nn'} \end{equation}\]

将谐振子的傅立叶展开代入哈密顿量，我们得到

(84)\[\begin{align} H = &\ \sum_{n=1}^N \left[ \frac{1}{2m} \pi_n^2 - \frac{K}{2} (\phi_{n+1}^2 + \phi_n^2 - 2 \phi_{n+1} \phi_n) \right] \\ = &\ \sum_{n=1}^N \left[ \frac{1}{2m} \pi_n^2 - K \phi_n^2 \right] + K \sum_{n=1}^N \phi_{n+1} \phi_n \end{align}\]

其中动能项给出

(85)\[\begin{align} \sum_{n=1}^N \frac{1}{2m} \pi_n^2 = &\ \sum_{n=1}^N \frac{1}{2m} \left( \frac{1}{\sqrt{N}} \sum_{q} e^{i q n a} \pi_q \right) \left( \frac{1}{\sqrt{N}} \sum_{q'} e^{i q' n a} \pi_q' \right) \\ = &\ \frac{1}{2 m N} \sum_{q, q'} \sum_{n=1}^N e^{i (q + q') n a} \pi_q \pi_{q'} \\ = &\ \frac{1}{2 m } \sum_{q, q'} \delta_{q, -q'} \pi_q \pi_{q'} \\ = &\ \frac{1}{2 m } \sum_{q} \pi_q \pi_{-q} \end{align}\]

类似的可以得到势能项非交叉项

(86)\[\begin{align} \sum_{n=1}^N K \phi_n^2 = &\ K \sum_{n=1}^N \left( \frac{1}{\sqrt{N}} \sum_{q} e^{i q n a} \phi_q \right) \left( \frac{1}{\sqrt{N}} \sum_{q'} e^{i q' n a} \phi_{q'} \right) \\ = &\ K \sum_{q} \phi_q \phi_{-q} \end{align}\]

而对于交叉项有

(87)\[\begin{align} K \sum_{n=1}^N \phi_{n+1} \phi_n = &\ K \sum_{n=1}^N \left( \frac{1}{\sqrt{N}} \sum_{q} e^{i q n a + i q a} \phi_q \right) \left( \frac{1}{\sqrt{N}} \sum_{q'} e^{i q' n a} \phi_{q'} \right) \\ = &\ K \sum_{q} \phi_q \phi_{-q} e^{i q a} \\ = &\ K \sum_{q} \phi_q \phi_{-q} \cos(q a) \end{align}\]

将三项求和后得到总哈密顿量

(88)\[\begin{split} \begin{align} H =&\ \sum_{q} \left[ \frac{1}{2m} \pi_q \pi_{-q} + K \left( 1 - \cos(q a) \right) \phi_q \phi_{-q}\right] \\ =&\ \sum_{q} \left[ \frac{1}{2m} \pi_q \pi_{-q} + \frac{1}{2} m \omega^2 \phi_q \phi_{-q}\right] \end{align} \end{split}\]

其中我们定义了谐振子频率

\[ \omega_q = \sqrt{\frac{2 K (1 - \cos(qa))}{m}} \]

当\(q\ll 1/a\)时，\(\cos(qa) \approx 1 - q^2 a^2/2\)，因此\(\omega_q \approx \sqrt{K/m} a |q|\)，这是一个近似的线性色散关系。

(88)并未将哈密顿量完全对角化。但我们仍然仿照单个简谐振子阶梯算符量子化的方式，引入如下产生湮灭算符：

(89)\[\begin{align} a_q =&\ \sqrt{\frac{m \omega_q}{2}} \left(\phi_q + \frac{i}{m \omega_q} \pi_q \right) \\ a_q^\dagger =&\ \sqrt{\frac{m \omega_q}{2}} \left(\phi_{-q} - \frac{i}{m \omega_q} \pi_{-q} \right) \end{align}\]

则

(90)\[\begin{align} \phi_q =&\ \sqrt{\frac{1}{2 m \omega_q}} \left( a_q + a_{-q}^\dagger \right) \\ \pi_q =&\ -i \sqrt{\frac{m \omega_q}{2}} \left( a_q - a_{-q}^\dagger \right) \end{align}\]

而原来的场和动量算符这时表示为

(91)\[\begin{split} \begin{align} \phi_n =&\ \frac{1}{\sqrt{N}} \sum_{q} e^{i q n a} \phi_q \\ =&\ \frac{1}{\sqrt{N}} \sum_{q} e^{i q n a} \sqrt{\frac{1}{2 m \omega_q}} \left( a_q + a_{-q}^\dagger \right) \\ \pi_n =&\ \frac{1}{\sqrt{N}} \sum_{q} e^{i q n a} \pi_q \\ =&\ \frac{1}{\sqrt{N}} \sum_{q} e^{i q n a} \left( -i \sqrt{\frac{m \omega_q}{2}} \left( a_q - a_{-q}^\dagger \right) \right) \end{align} \end{split}\]

如果我们要求产生湮灭算符满足对易关系

(92)\[\begin{equation} [a_q, a_{q'}^\dagger] = \hbar \delta_{qq'} \,, \quad [a_q, a_{q'}] = [a_q^\dagger, a_{q'}^\dagger] = 0 \end{equation}\]

则有

(93)\[\begin{equation} [\phi_n, \pi_m] = i \hbar \delta_{nm} \end{equation}\]

这正是正则量子化的要求，因此我们对产生湮灭算符对易关系的假定是自洽的。

将哈密顿量用产生湮灭算符表示，我们得到：

(94)\[\begin{align} H = &\ \sum_{q} \left[ \frac{1}{2m} \pi_q \pi_{-q} + \frac{1}{2} m \omega_q^2 \phi_q \phi_{-q}\right] \\ = &\ \sum_{q} \left[ \frac{1}{2m} \left( -i \sqrt{\frac{m \omega_q}{2}} \left( a_q - a_{-q}^\dagger \right) \right) \left( - i \sqrt{\frac{m \omega_q}{2}} \left( a_{-q} - a_q^\dagger \right) \right) + \frac{1}{2} m \omega_q^2 \left( \sqrt{\frac{1}{2 m \omega_q}} \left( a_q + a_{-q}^\dagger \right) \right) \left( \sqrt{\frac{1}{2 m \omega_q}} \left( a_{-q} + a_q^\dagger \right) \right) \right] \\ = &\ \sum_{q} \left[ \frac{1}{4} \omega_q \left( - a_q a_{-q} + a_{q} a_{-q} - a_{-q}^\dagger a_{q}^\dagger + a_{-q}^\dagger a_{-q}^\dagger \right) + \frac{1}{2} \omega_q \left( a_q a_q^\dagger + a_{-q}^\dagger a_{-q} \right) \right] \\ = &\ \sum_{q} \omega_q \hbar \left( a_q^\dagger a_q + \frac{1}{2} \right) \end{align}\]

我们看到这时哈密顿量被写成了具有不同动量的单个哈密顿量的叠加：

(95)\[\begin{equation} H = \sum_{q}H_q \end{equation}\]

其中

(96)\[\begin{equation} H_q = \omega_q \hbar \left( a_q^\dagger a_q + \frac{1}{2} \right) \end{equation}\]

其中针对单个\(H_q\)可以构建对应的Fock空间表示\(|n_q \rangle\)，而完整的哈密顿量的本征态则是所有\(H_q\)的本征态的直积：

(97)\[\begin{equation} |n_{q_1}, n_{q_2}, \cdots, n_{q_k} \rangle = |n_{q_1} \rangle \otimes |n_{q_2} \rangle \otimes \cdots \otimes |n_{q_k} \rangle \end{equation}\]

这个态的能量本征值为

(98)\[\begin{equation} E = \sum_{q} \omega_q \hbar \left( n_q + \frac{1}{2} \right) \end{equation}\]

直此，我们利用阶梯算符方法解出了一维耦合谐振子问题。整个过程不涉及复杂的矩阵对角化，而是通过对产生湮灭算符的对易关系的假定，直接得到了哈密顿量的对角化形式。这种方法在量子场论中有着重要的应用。

虽然阶梯算符方法解出了耦合谐振子的能谱，但同学们自然会问，这个解的物理意义是什么？我们最初的物理量\(\phi_n\)代表了第\(n\)个谐振子的位移量，具有明确的物理意义。但\(\phi_q\)和\(a_q\)代表什么？答案是，\(a_{q}^\dagger\)作用到真空态上得到了一个动量为\(q\)的准激发/粒子，在晶格振动中称作声子。准粒子是谐振子链的集体激发，他不对应某个单个谐振子的位移。特别是，准粒子的概念在谐振子数目\(N\)很大时是很形象的，如下面网络博主ZAPPhysics的动画所示(https://github.com/ZAPPhysics/QFT_Sims)：

Note

例子：德拜理论

上面的结果有一个直接的应用。将其推广到三维晶格振动问题只需作少许改动。三维的声子存在横波和纵波两类极化，每种极化对应一个谐振子哈密顿量，能量本征值写为

(99)\[\begin{equation} E = \sum_{\boldsymbol{q}, \lambda} \omega_{\boldsymbol{q}, \lambda} \hbar \left( n_{\boldsymbol{q}} + \frac{1}{2} \right) \end{equation}\]

其中\(\lambda\)可取两个横极化和一个纵极化。为了简单起见，我们假设特征频率与极化无关，\(\omega_{\boldsymbol{q}, \lambda} = \omega_{\boldsymbol{q}} = v |\boldsymbol{q}|\)。

晶格中的声子属于玻色子，声子数遵从玻色-爱因斯坦分布：

(100)\[\begin{equation} n_{\boldsymbol{q}} = \frac{1}{e^{\beta \hbar \omega_{\boldsymbol{q}}} - 1} \end{equation}\]

其中\(\beta = 1/(k_B T)\)，\(T\)是温度，\(k_B\)是玻尔兹曼常数，因此能量为

(101)\[\begin{equation} E =3 \sum_{\boldsymbol{q}} \hbar \omega_{\boldsymbol{q}} \left( \frac{1}{e^{\beta \hbar \omega_{\boldsymbol{q}}} - 1} + \frac{1}{2}\right) \end{equation}\]

在热力学极限\(N\to \infty\)下，我们可以将求和转化为积分：

(102)\[\begin{equation} \sum_{\boldsymbol{q}} \to V \int \frac{d^3 q}{(2\pi)^3} \end{equation}\]

因此

(103)\[\begin{equation} E = 3 V \int \frac{d^3 q}{(2\pi)^3} \hbar \omega_{\boldsymbol{q}} \left( \frac{1}{e^{\beta \hbar \omega_{\boldsymbol{q}}} - 1} + \frac{1}{2}\right) \end{equation}\]

系统总自由度个数在热力学极限下可以写为

(104)\[\begin{equation} N = \sum_{\boldsymbol{q}} \to V \int \frac{d^3 q}{(2\pi)^3} = \frac{V}{2 \pi^2} \int_0^{q_D} q^2 dq = \frac{V}{6 \pi^2} q_D^3 \end{equation}\]

其中\(q_D\)是截断频率。实验上的一个可观测量是比热容，它定义为单位比热容随温度的变化率：

(105)\[\begin{equation} c_V = \frac{dE}{N dT} \end{equation}\]

令

(106)\[\begin{equation} \beta \hbar \omega_{\boldsymbol{q}} = z \,, \qquad d z = \frac{\hbar v}{k_B T} dq \end{equation}\]

则

(107)\[\begin{align} c_V = &\ \frac{6 \pi^2}{V q_D^3} \frac{d}{dT} \left( 3 V \int \frac{q^2 d q}{2\pi^2} \hbar v q \left( \frac{1}{e^{z} - 1} + \frac{1}{2}\right) \right) \\ =&\ \frac{9 \hbar v}{q_D^3} \int_0^{q_D} q^3 dq \frac{d}{dT} \frac{1}{e^{z} - 1} \\ =&\ \frac{9 \hbar v}{q_D^3} \int_0^{q_D} q^3 dq \frac{e^z}{(e^z - 1)^2} \frac{\hbar v q}{k_B T^2} \\ =&\ \frac{9 \hbar^2 v^2}{k_B T^2 q_D^3} \int_0^{q_D} \frac{q^4 e^{z} dq}{(e^{z} - 1)^2} \\ =&\ \frac{9 \hbar^2 v^2}{k_B T^2 q_D^3} \left( \frac{k_B T}{\hbar v} \right)^5 \int_0^{T_D/T} \frac{z^4 e^z dz}{(e^{z} - 1)^2} \end{align}\]

其中\(T_D = \hbar v q_D/k_B\)是德拜温度。上式可以化简作

(108)\[\begin{equation} c_V = 9 k_B \frac{T^3}{T_D^3} \int_0^{T_D/T} \frac{z^4 e^z dz}{(e^{z} - 1)^2} \end{equation}\]

在低温时，\(T_D/T \to \infty\)，我们可以近似积分上限为无穷，此时

(109)\[\begin{equation} c_V \to 9 k_B \frac{T^3}{T_D^3} \int_0^{\infty} \frac{z^4 e^z dz}{(e^{z} - 1)^2} \simeq k_B \frac{T^3}{T_D^3} \frac{12 \pi^4}{5} \end{equation}\]

而在高温时，\(T_D/T \to 0\)，我们将被积函数泰勒展开，

(110)\[\begin{equation} \frac{z^4 e^z}{(e^z - 1)^2} \simeq z^2 + \cdots \end{equation}\]

因此

(111)\[\begin{equation} c_V \to 3 k_B + \cdots \end{equation}\]

高温极限下的结果与杜隆-泊替定律一致。

连续极限

让我们稍稍回顾一下上面的讨论。在讨论一维原子链时，我们将原子间距\(a\)作为一个固定的参数。但实际上，原子间距\(a\)是一个连续的变量，我们可以考虑连续极限\(a \to 0\)，但保留长度\(L\)不变。同时，我们将一维原子链推广到三维。我们可以将分立的晶格位移\(\phi_{\boldsymbol{n}}\)看作是连续的场\(\phi(\boldsymbol{x})\)。作为我们出发点的哈密顿量

(112)\[\begin{equation} H = \sum_{n=1}^N \left[ \frac{\pi_n^2}{2m} + \frac{K}{2} (\phi_{n+1} - \phi_n)^2 \right] \end{equation}\]

等价的，我们讨论的系统的拉格朗日量为：

(113)\[\begin{align} L =& \ \sum_{n=1}^N \pi_n \dot \phi_n - H \\ =& \ \sum_{n=1}^N \left[ \frac{m \dot\phi_n^2}{2} - \frac{K}{2} (\phi_{n+1} - \phi_n)^2 \right] \end{align}\]

我们求解这个系统的本质方式是对动力学坐标\(\phi_n\)和动量\(\pi_n\)作了如下离散傅立叶变换(式(91))：

(114)\[\begin{align} \phi_n =&\ \frac{1}{\sqrt{N}} \sum_{q} e^{i q n a} \phi_q \\ =&\ \frac{1}{\sqrt{N}} \sum_{q} e^{i q n a} \sqrt{\frac{1}{2 m \omega_q}} \left( a_q + a_{-q}^\dagger \right) \\ \pi_n =&\ \frac{1}{\sqrt{N}} \sum_{q} e^{i q n a} \pi_q \\ =&\ \frac{1}{\sqrt{N}} \sum_{q} e^{i q n a} \left( -i \sqrt{\frac{m \omega_q}{2}} \left( a_q - a_{-q}^\dagger \right) \right) \end{align}\]

我们也把这个变换称作模式分解。

下面我们将这个操作推广到三维，并取连续极限\(a\to 0\)。为此，我们将三维格点求和写作积分：

(115)\[\begin{equation} \sum_{n_1, n_2, n_3} \to \frac{1}{a^3} \sum_{n_1, n_2, n_3} a^3 = \frac{1}{a^3} \int d^3 x \end{equation}\]

因此在三维连续极限下可以写为

(116)\[\begin{equation} H = \frac{1}{a^3} \int_V d^3 x \left[ \frac{1}{2m a^3} \pi(x)^2 + \frac{K}{2a} (\nabla \phi(x))^2 \right] \end{equation}\]

而对应的拉格朗日量：

(117)\[\begin{equation} L = \frac{1}{a^3} \int d^3 x \pi(x) \dot \phi(x) - H = \int_V d^3 x \left[ \frac{m \dot\phi^2}{2 a^3} - \frac{K}{2a} (\nabla \phi(x))^2 \right] \end{equation}\]

我们对场作重新定义

(118)\[\begin{equation} \phi \to \sqrt{\frac{a^3}{m}} \phi' \end{equation}\]

这时拉氏量可以写为

(119)\[\begin{equation} L = \int_V d^3 x\, {\cal L(x)} \end{equation}\]

其中\({\cal L}\)是连续极限下晶格振动的拉氏密度：

(120)\[\begin{equation} {\cal L} = \frac{ \dot\phi'^2}{2} - \frac{c_s^2}{2} (\nabla \phi'(x))^2 \end{equation}\]

其中\(c_s = \sqrt{K/m} a\)是晶格声速。这是一个经典连续场论，尽管它不是洛伦兹不变的，但它提供了如何量子化一个经典场论的范例。

动量\(q\)积分的连续化可以写为：

(121)\[\begin{equation} \sum_{q_1, q_2, q_3} = \left(\frac{L}{2 \pi} \right)^3 \sum_{q_1, q_2, q_3} \left(\frac{2 \pi}{L}\right)^3 \to V \int \frac{d^3 q}{(2\pi)^3} \end{equation}\]

(91)中给出的场的分立傅立叶变换在连续极限下可以写为

(122)\[\begin{align} \phi(x) =&\ \frac{V}{\sqrt{N^3}} \int \frac{d^3 q}{(2\pi)^3} \phi_q e^{i \boldsymbol{q} \cdot \boldsymbol{x}} \\ =&\ \sqrt{V a^3} \int \frac{d^3 q}{(2 \pi)^3 \sqrt{2 m \omega_q}} \left(a_{\boldsymbol{q}} + a_{- \boldsymbol{q}}^\dagger \right) e^{i \boldsymbol{q} \cdot \boldsymbol{x} } \\ =&\ \sqrt{V a^3} \int \frac{d^3 q}{(2 \pi)^3 \sqrt{2 m \omega_q}} \left(a_{\boldsymbol{q}} e^{i \boldsymbol{q} \cdot \boldsymbol{x} } + a_{ \boldsymbol{q}}^\dagger e^{-i \boldsymbol{q} \cdot \boldsymbol{x} } \right) \end{align}\]

对重定义后的场则有

(123)\[\begin{equation} \phi'(x) = \sqrt{V} \int \frac{d^3 q}{(2 \pi)^3} \frac{1}{\sqrt{2 \omega_q}} \left(a_{\boldsymbol{q}} e^{i \boldsymbol{q} \cdot \boldsymbol{x} } + a_{ \boldsymbol{q}}^\dagger e^{-i \boldsymbol{q} \cdot \boldsymbol{x} } \right) \end{equation}\]

但不要忘记我们此时的产生湮灭算符满足的对易关系仍然是分立形式的：

(124)\[\begin{equation} [a_{\boldsymbol{q}}, a_{\boldsymbol{q}'}^\dagger] = \hbar \delta_{\boldsymbol{q} \boldsymbol{q}'} \end{equation}\]

它满足的约束是

(125)\[\begin{equation} \sum_{\boldsymbol{q}} [a_{\boldsymbol{q}}, a_{\boldsymbol{q}'}^\dagger] = \hbar \end{equation}\]

将求和用连续极限表则有

(126)\[\begin{equation} V \int \frac{d^3 q}{(2\pi)^3} [a_{\boldsymbol{q}}, a_{\boldsymbol{q}'}^\dagger] = \hbar \end{equation}\]

这个式子告诉我们产生湮灭算符对易关系的恰当连续极限应表示为

(127)\[\begin{equation} [a_{\boldsymbol{q}}, a_{\boldsymbol{q}'}^\dagger] = \frac{\hbar}{V} (2\pi)^3 \delta^3(\boldsymbol{q} - \boldsymbol{q}') \end{equation}\]

如果我们重新定义产生湮灭算符：

(128)\[\begin{equation} a'_{\boldsymbol{q}} = \sqrt{\frac{V}{(2\pi)^3}} a_{\boldsymbol{q}} \qquad {a'}_{\boldsymbol{q}}^\dagger = \sqrt{\frac{V}{(2\pi)^3}} a_{\boldsymbol{q}}^\dagger \end{equation}\]

则对易关系可以写为

(129)\[\begin{equation} [a'_{\boldsymbol{q}}, {a'}_{\boldsymbol{q}'}^\dagger] = \hbar \delta^3(\boldsymbol{q} - \boldsymbol{q}') \end{equation}\]

而我们场的展开可以写为

(130)\[\begin{equation} \phi'(x) = \int \frac{d^3 q}{(2 \pi)^3} \frac{1}{\sqrt{ (2 \pi)^ 3 2 \omega_q}} \left(a'_{\boldsymbol{q}} e^{i \boldsymbol{q} \cdot \boldsymbol{x} } + {a'}_{ \boldsymbol{q}}^\dagger e^{-i \boldsymbol{q} \cdot \boldsymbol{x} } \right) \end{equation}\]

而正则动量的展开为

(131)\[\begin{equation} \pi'(x) = - i \int \frac{d^3 q}{\sqrt{(2 \pi)^3}} \sqrt{\frac{\omega_q}{2}} \left(a'_{\boldsymbol{q}} e^{i \boldsymbol{q} \cdot \boldsymbol{x} } - {a'}_{ \boldsymbol{q}}^\dagger e^{-i \boldsymbol{q} \cdot \boldsymbol{x} } \right) \end{equation}\]

这个结果给出了非相对论性声子场的正则量子化模式展开公式。今后，为了简化起见，我们将忽略掉场、动量和产生湮灭算符上的一撇，直接将其作为我们的基本量。